矩阵的几种分解方式

A = LU

这实际上就是我们解矩阵方程组一般使用的方式，比如方程组是：

a_{11}x_1 + a_{12}x_2 + \cdots + a_{1n}x_n = b_1 \\ a_{21}x_1 + a_{22}x_2 + \cdots + a_{2n}x_n = b_2 \\ \cdots \\ a_{n1}x_1 + a_{n2}x_2 + \cdots + a_{nn}x_n = b_n \\

我们一般把它写成增广矩阵：

\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} & b_1 \\ a_{21} & a_{22} & \cdots & a_{2n} & b_2 \\ & \cdots & \\ a_{n1} & a_{n2} & \cdots & a_{nn} & b_n \\ \end{bmatrix}\\

然后化简成阶梯型矩阵的形式，这个时候可以方便的算出 x_n ,然后再往上代回，逐渐得到所有的x。

如果我们实际来 coding，可能会出现的问题：

a_{11} 为0， 或者 a_{11} = \varepsilon \ll 1 ,那么我们化简第二行时 a_{22} - \frac{a_{21}}{a_{11}} * a_{12} 可能会误差很大

解决的办法就是行交换，把比较大的pivot放在前面。其实这个我们手动解 A\mathbf{x} = \mathbf{b} 的时候就会这样做。

这个方法叫做 Gaussian elimination with partial pivoting (GEPP). 实际上 Matlab 中用的一般也就是这个办法来解 A\mathbf{x} = \mathbf{b} , 当然在 Matlab 中我们一般如果要解答可以直接用 x = A\b 就可以知道了，不过我们如果想知道的明确 L，U矩阵我们可以 [L, U] = lu(A). 当然其实严密一点来说是如果我们用 [L,U] = lu(A)得到的这个L是一个permutaed lower triangle matrix，再加上交换才是严格的lower triangle，也就是 [L, U, P] = lu(A).

比如矩阵:

>> A = [1 2 -3; -3 -1 1; 1 -1 1];
>> [L, U] = lu(A)

L =

   -0.3333    1.0000         0
    1.0000         0         0
   -0.3333   -0.8000    1.0000


U =

   -3.0000   -1.0000    1.0000
         0    1.6667   -2.6667
         0         0   -0.8000

>> [L, U, P] = lu(A)

L =

    1.0000         0         0
   -0.3333    1.0000         0
   -0.3333   -0.8000    1.0000


U =

   -3.0000   -1.0000    1.0000
         0    1.6667   -2.6667
         0         0   -0.8000


P =

     0     1     0
     1     0     0
     0     0     1

A = QR

Q 代表的是正交矩阵，这里的 R 是 upper triangle 矩阵：

>> [Q,R] = qr(A)

Q =

   -0.3015   -0.7675    0.5657
    0.9045   -0.0426    0.4243
   -0.3015    0.6396    0.7071


R =

   -3.3166   -1.2060    1.5076
         0   -2.1320    2.8995
         0         0   -0.5657

我们可以通过 Gram–Schmidt 完成 QR 分解。

正交矩阵当然是具有很多很好特性的矩阵，比如：

• QQ^T = I
• det(Q) = ±1, 如果 det(Q) = 1 则为旋转变换，说起旋转变换又会想到SO(n) 李群和李代数
• 可以给我们提供一组正交基

\mathbf{S = QΛQ^T}

当矩阵是一个实对称矩阵S（symmetric）的时候，我们可以把它分解成：

S = Q \Lambda Q^T \\

正交矩阵Q、 对角矩阵Λ（特征值）、正交矩阵的转置 Q^T 。

这个分解叫特征分解（Eigendecomposition），又称谱分解（Spectral decomposition），因为 Q 中是特征向量， Λ 中是特征值， q_1, \cdots, q_n 是跟 \lambda_1, \cdots, \lambda_n 这些特征值对应的特征向量。

当然在 Matlab中我们还是用 [V, D] = eig(S) 可以得到它的对应矩阵 Q 和 Λ.

>> A = [1 4 5; 4 2 6; 5 6 3];
>> issymmetric(A)

ans =

  logical

   1

>> [V, D] = eig(A)

V =

    0.3130    0.8096    0.4966
    0.5774   -0.5774    0.5774
   -0.7541   -0.1060    0.6481


D =

   -3.6687         0         0
         0   -2.5073         0
         0         0   12.1760

\mathbf{A = U \Sigma V^T}

SVD - 奇异值分解（singular value decomposition），之前写过PCA(主成分分析) 和 SVD (奇异值分解)。

Matlab 中使用：

>> [U, S, V] = svd(A)

U =

   -0.7795   -0.4214    0.4634
    0.6107   -0.6760    0.4125
    0.1394    0.6045    0.7843


S =

    4.5807         0         0
         0    2.6280         0
         0         0    0.3323


V =

   -0.5397    0.8413    0.0309
   -0.5041   -0.2936   -0.8122
    0.6743    0.4539   -0.5825

\mathbf{A = LL^T}

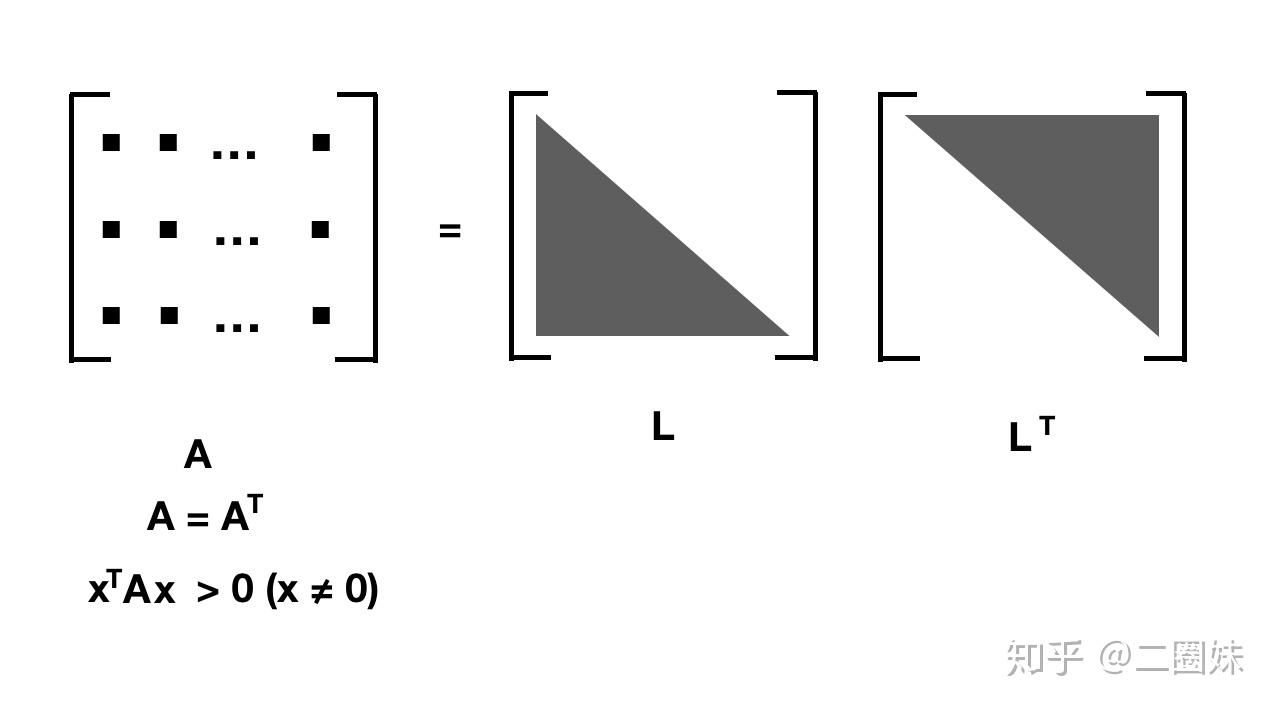
Cholesky分解，当 A 是一个SPD (real Symmetric positive definite matrix）的时候，我们可以把它分解成 lower triangle 矩阵 L 和它的转置也就是 upper triangle L^T .

>> A = [4 12 -16; 12 37 -43; -16 -43 98];
>> R = chol(A)

R =

     2     6    -8
     0     1     5
     0     0     3

>> R'*R

ans =

     4    12   -16
    12    37   -43
   -16   -43    98

A=XΛX^{−1}

如果 A 可以对角化，那么 A 可以分解成 A=XΛX^−1 。 依旧可以使用特征值分解来解决这个问题。