【其实贼简单】拉普拉斯算子和拉普拉斯矩阵

内容同步发布于科创社区机器学习板块，欢迎支持呀～

在机器学习、多维信号处理等领域，凡涉及到图论的地方，相信小伙伴们总能遇到和拉普拉斯矩阵和其特征值有关的大怪兽。哪怕过了这一关，回想起来也常常一脸懵逼，拉普拉斯矩阵为啥被定义成 L = D - W ？这玩意为什么冠以拉普拉斯之名？为什么和图论有关的算法如此喜欢用拉普拉斯矩阵和它的特征值？

最近读论文的时候，刚好趁机温习了一下相应的内容，寻本朔源一番，记录下来，希望大家阅读之后，也能够有个更加通透的理解。

要讲拉普拉斯矩阵，就要从拉普拉斯算子讲起，要讲拉普拉斯算子，就要从散度讲起～

于是我们从散度开始，发车啦～～～

通量与散度

首先我们来看一道初中物理题：

小明乘帆船出行，刮来一阵妖风，假设帆的面积为 S , 和妖风的夹角为 \alpha ，妖风在每单位面积上的垂直风压为 P ，求妖风对帆的推动力

那么聪明伶俐（？）的我们一定知道，这道题的答案应该是 F = S \times P \times \sin(\alpha) 。

如果我们用 \vec{A} 表示风的向量（且 ||\vec{A}|| = P ），用 \vec{n} 表示帆的法向量，那么 \vec{n} 与风的夹角即是 \frac{\pi}{2} - \alpha ，结合高中数学知识我们知道上述公式也可以写成

F = S \cdot \vec{A} \cdot \vec{n}

。。。

如果我们现在再把题目弄复杂一点，假设船帆不是一个平面，而是一个空间中的曲面 \Sigma ，在 \Sigma 所在的每一点（面积微元 dS ）处，其法向量为 \vec{n} ，且空间中存在的风为 \vec{A} ，根据大学数学知识我们可以得到：

F = \iint_\Sigma{\vec{A} \cdot \vec{n} dS}

于是我们就得到了通量 \Phi 的定义， \Phi_A(\Sigma) = \iint_\Sigma{\vec{A} \cdot \vec{n} dS}

。。。

那么如果我们有一个封闭曲面呢，比如：

此时我们指定曲面每一点处的法向量为该点朝外的向量：

红色箭头为法向量，注意在上面的例子中风与帆的比喻并不完全恰当，在计算通量的时候一般我们认为向量场会穿过曲面，而非被挡住

于是我们有

\Phi_A(\Sigma) = \oint_\Sigma{\vec{A} \cdot \vec{n} dS}

对于上图，根据向量乘法的基本原理，聪明的我们很容易知道，对于射入曲面的那一部分（左半边），其通量为负，而对于射出曲面的那一部分（右半边），其通量为正。

更进一步的思考我们可以得出，相互抵消后，这一曲面上的总通量为 0

。。。

接下来我们看下一张图：

显然，在这一向量场中，红色曲面上的总通量为负，而绿色曲面上的总通量为正。 那么我们不断缩小这两个曲面，直至其无限接近一个点 \{x\} ，并将其总通量除以曲面所围成的体积 \delta V ，得到：

\nabla A = \lim_{\delta V \rightarrow {x}}\frac{\Phi_A(\Sigma)}{\delta V} ，

我们便得到了点 \{x\} 处的散度。

。。。

根据上面的分析，我们不难看出，在红圈所在圆心处的散度为负，而绿圈圆心处的散度为正。

结合上述定义，我们知道，散度衡量了一个点处的向量场是被发射还是被吸收，或者说，对于散度为正的点，散度越大，意味着相应的向量场越强烈地在此发散，而对于散度为负的点，意味着相应的向量场在此汇聚

嗯，就这么简单～ XD

拉普拉斯算子

接下来就是我们可爱的拉普拉斯算子啦～～

根据定义，函数 f 的拉普拉斯算子 \nabla^2 f 又可以写成 \nabla \cdot \nabla f ，其被定义为函数 f 梯度的散度。

那么这又是什么意思呢？

我们知道，在直角坐标系下，一个函数 f(x,y,z) 在 (x_0, y_0, z_0) 处的梯度是一个向量 (\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}, \frac{\partial f}{\partial z})|_{x=x_0, y=y_0, z=z_0} ，

于是函数 f 的梯度函数 \nabla f = \frac{\partial f}{\partial x} \cdot \vec{i} + \frac{\partial f}{\partial y} \cdot \vec{j} + \frac{\partial f}{\partial z} \cdot \vec{k}

就构成了一个在三维空间下的向量场。

于是乎，我们对这一向量场 \nabla f 求散度 \nabla \cdot \nabla f ，即得到了 f 的拉普拉斯算子 \nabla^2 f 。

为什么要这样做呢？

让我们想像一座山，根据梯度的定义，在山峰周围，所有的梯度向量向此汇聚，所以每个山峰处的拉普拉斯算子为负；而在山谷周围，所有梯度从此发散，所以每个山谷处的拉普拉斯算子为正。所以说，对于一个函数，拉普拉斯算子实际上衡量了在空间中的每一点处，该函数梯度是倾向于增加还是减少

歪个楼，描述物理系统最优美的公式之一拉普拉斯方程， \nabla^2 f = 0 ，大家可以想一想，这一公式表达了物理系统怎么样的特征呢？

图论下的函数

我们知道，互相连接的节点可以构成一张图，其中包含所有点构成的集合 V , 和所有边构成的集合 E 。

对于实数域上的函数 y = f(x) ，我们可以理解为一种对于 x 的映射，将每个可能的 x \in X 映射到一个对应的 y \in Y 上（ f: X \rightarrow Y ）。

相应地，我们也可以定义一个图函数 F_G: V \rightarrow R ，使得图上的每一个节点 v \in V ，都被映射到一个实数 R 上。

比如说，假设我们有一个这样的社交网络图谱：

假设说每一条边的权值对应两个人之间信息的流通程度。现在我们想要分析这个社交网络上的信息传播，我们不仅需要知道信息流通的程度，我们还要知道每个人发动态的活跃程度，于是我们现在给这个图一个函数 F_G ，使得：

F_G(A) = 3, F_G(B) = 5, F_G(C) = -2, F_G(D) = 1, F_G(E) = -5

这里的负数似乎可以理解为， C 和 E 是谣言终结者，可以阻止信息的传播～

那么我们得到这样一张图：

图函数的梯度

我们定义了图论的函数，那么应该如何给图论下的函数定义梯度呢？

我们记得，梯度的意义在于，衡量函数在每一个点处，在每个正交方向上的变化，如 f(x, y,z) 的梯度在 x 方向的分量 \frac{\partial f}{\partial x} = \frac{f(x + dx) - f(x)}{(x + dx) - x}

在图论中，我们认为一个节点沿着每一条边通向它的相邻节点，而每两条边之间互相并没有什么关系，也就是说我们认为这个节点的每一条边互相都是正交的

并且对于两个节点，我们定义其距离 d 为其边权值的倒数（比如上面社交网络的例子，我们可以认为，两个人的信息流通程度越低，两个人的友谊就“越远”）

那么对于一个节点 v_0 ，我们认为其梯度在一条通向 v_1 的边 e_{01} 上的分量为

\frac{(F_G(v_0) - F_G(v_1))}{d_{01}} = (F_G(v_0) - F_G(v_1)) \cdot e_{01}

（其中 d_{01} 为 v_0 到 v_1 的距离），

为了计算梯度，我们给出一个这样的矩阵：

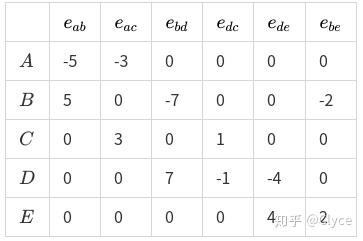
每一行代表一个点，每一列代表一条边，使得对于每个点每条边，如果该条边从该点发射出去，且权值为 X ，则将矩阵中对应的这一元素置为 +X ，如果该条边指向该点，则将对应的元素置为 -X

具体到上面社交网络的例子，我们有相应的矩阵 K_G ：

我们又有关于图函数 F_G 的列向量 f_G ：

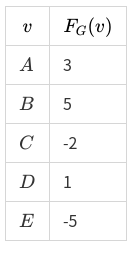
我们试着计算 K^T_G \times f_G ：

\begin{pmatrix} -5 & 5 & 0 & 0 & 0 \\ -3 & 0 & 3 & 0 & 0 \\ 0 & -7 & 0 & 7 & 0 \\ 0 & 0 & 1 & -1 & 0 \\ 0 & 0 & 0 & -4 & 4 \\ 0 & -2 & 0 & 0 & 2 \\ \end{pmatrix} \times \begin{pmatrix} 3 \\ 5 \\ -2 \\ 1 \\ -5 \\ \end{pmatrix} = \begin{pmatrix} 10 \\ -15 \\ -28 \\ -3 \\ -24 \\ -20 \\ \end{pmatrix}

经过观察我们可以知道，最后计算结果的向量，即是整个图 G 在 F_G 函数上的梯度 \nabla_G F_G ，其中每一行，为该梯度在一条边上的分量。

所以对于图 G ，我们有 \nabla_G = K^T_G ,使得 \nabla_G F_G = K^T_G \times f_G

拉普拉斯算子与拉普拉斯矩阵

我们记得在函数中，拉普拉斯算子的定义为函数梯度的散度，即每一点上其梯度的增加/减少，那么对于图函数，其每一“点”即为每个“节点”，其梯度的散度该怎么定义呢？

我们几乎可以立刻可以想到，图函数每一点上梯度的散度，即是从该节点射出的梯度，减去射入该节点的梯度，那么我们几乎又可以立即想到（？），根据这样的定义去计算散度，只要把原来的梯度再左乘一个这样的矩阵就可以啦：

每一行代表一个点，每一列代表一条边，使得对于每个点每条边，如果该条边从该点发射出去，则将矩阵中对应的这一元素置为 +1 ，如果该条边指向该点，则将对应的元素置为 -1

命名这一矩阵为 K_G'

也就是说，我们把 K_G 的每个元素，正的变成1，负的变成-1，就得到了 K_G'

\begin{pmatrix} -1 & -1 & 0 & 0 & 0 & 0 \\ 1 & 0 & -1 & 0 & 0 & -1 \\ 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & -1 & -1 & 0 \\ 0 & 0 & 0 & 0 & 1 & 1 \\ \end{pmatrix} \times \begin{pmatrix} 10 \\ -15 \\ -28 \\ -3 \\ -24 \\ -20 \\ \end{pmatrix} = \begin{pmatrix} 5 \\ 58 \\ -18 \\ -1 \\ -44 \end{pmatrix}

那么，

\begin{align} \nabla_G^2 F_G & = K_G' \times \nabla_G F_G \\ & = K_G' \times (K_G^T \times f_G) \\ & = (K_G'K_G^T)f_G \end{align}

于是我们得到了图论函数的拉普拉斯算子 \nabla^2 = K_G'K_G^T ，即我们常说的拉普拉斯矩阵。

注意在我们上面的范例中，将任意一条边的方向反转，等价于在 K_G 的一列上乘以 -1 ，这种情况下最终 K_G'K_G^T 不会改变，也就是说拉普拉斯矩阵的值与图中每一条边的方向无关，所以拉普拉斯矩阵一般用来表述无向图

计算 K_G'K_G^T 的值，我们得到矩阵：

\begin{pmatrix} 8 & -5 & -3 & 0 & 0 \\ -5 & 14 & 0 & -7 & -2 \\ -3 & 0 & 4 & -1 & 0 \\ 0 & -7 & -1 & 12 & -4 \\ 0 & -2 & 0 & -4 & 6 \\ \end{pmatrix}

注意到这一对称矩阵，对角线即是每个点的度，而其余的元素，则是负的邻接矩阵，于是乎我们得到了拉普拉斯矩阵的经典算式：

L = D - W

（至于外面的各种资料为什么往往只使用 L = D - W 而非 L = K_G' K^T_G ，个人认为是因为前者只涉及减法，计算远远快于后者，所以程序中一般使用前者。但是为了理解拉普拉斯矩阵的意义，对后者的了解在我看来是必须的）

拉普拉斯矩阵的重要性质

拉普拉斯矩阵之所以如此常用，是因为其一大重要性质： 拉普拉斯矩阵的 n 个特征值 \lambda_1, \lambda_2, ..., \lambda_n 都是非负值，且有 0= \lambda_1 \leq \lambda_2 \leq ... \leq \lambda_n

同时，我们引入关于矩阵 L 和 h 的瑞利熵的概念： R(L,h) = \frac{h^*Lh}{h^*h}

其中 h^* 为 h 的共轭矩阵，对于 h 为实数矩阵的情况下 h^* = h^T

而通过拉格朗日乘子法可以得出，瑞利熵的一个非常重要的特点就是： 瑞丽熵的最大值，等于 L 的最大特征值，瑞利熵的最小值，等于 L 的最小特征值

再看看图算法中对于拉普拉斯矩阵 L 的运算中常常出现的 f^TLf ，结合上文所述的拉普拉斯矩阵的重要性质，那么拉普拉斯矩阵在各种图算法中的应用，想必大家也能够理解啦～