卷积神经网络(CNN)反向传播算法推导
在之前的文章中我介绍了多层感知机反向传播的数学推导,主要是用数学公式来进行表示的,在全连接神经网络中,它们并不复杂,即使是纯数学公式也比较好理解。而卷积神经网络相对比较复杂,在本篇文章中我们将从直观感受和数学公式两方面来介绍CNN反向传播算法的推导。
首先我给大家介绍一下我分析delta误差反向传播过程的简单方法,如果神经网络l+1层某个结点的delta误差要传到l层,我们就去找前向传播时l+1层的这个结点和第l层的哪些结点有关系,权重是多少,那么反向传播时,delta误差就会乘上相同的权重传播回来。
假设第l层有一个结点a,l+1层有一个结点b。两个结点间的连接权重为w。如果前向传播时,结点a对结点b的影响是 wa 。而反向传播时,结点b的delta误差 \delta_b 对结点a的delta误差 \delta_a 的影响是 w\delta_b 。它们的系数都为两结点之间的连接权重。
卷积神经网络前向传播过程简要介绍
在理解卷积神经网络的反向传播之前,我们需要对卷积、池化以及卷积神经网络前向传播过程作一个简要的回顾。
卷积运算介绍
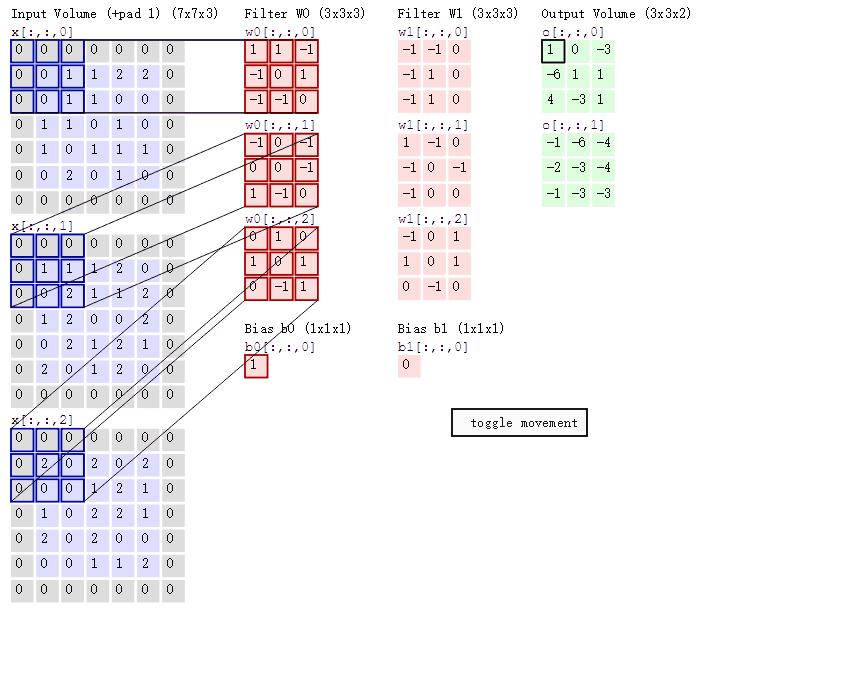
在卷积神经网络中,所谓的卷积运算,其实并不是严格的数学意义上的卷积。深度学习中的卷积实际上是信号处理和图像处理中的互相关运算,它们二者之间有细微的差别。深度学习中的卷积(严格来说是互相关)是卷积核在原始图像上遍历,对应元素相乘再求和,得到的新图像在尺寸上会有减小。可以通过下图直观的去理解。假设输入图像的有m行,n列,卷积核的尺寸为filter_size×filter_size,输出图像的尺寸即为(m-filter_size+1)×(n-filter_size+1)

在全连接神经网络,图像数据以及特征是以列向量的形式进行存储。而在卷积神经网络中,数据的格式主要是以张量(可以理解为多维数组)的形式存储。图片的格式为一个三维张量,行×列×通道数。卷积核的格式为一个四维张量,卷积核数×行×列×通道数。
卷积操作是每次取出卷积核中的一个,一个卷积核的格式为三维,为行×列×通道数。对应通道序号的图片与卷积核经过二维卷积操作后(即上图所示操作),得到该通道对应的卷积结果,将所有通道的结果相加,得到输出图像的一个通道。每个卷积核对应输出图像的一个通道,即输出图像的通道数等于卷积核的个数。
这里概念有一点绕,但是卷积神经网络中所谓张量的卷积,本质上是进行了一共卷积核数×通道数次二维卷积操作。每一个卷积核对应卷积结果的一个通道,每一个卷积核的通道对应原始图片的一个通道。这个操作和一个列向量乘上一个矩阵得到一个新的列向量有相似的地方。
下图直观地展示了张量卷积具体操作过程:
池化操作介绍
所谓的池化,就是对图片进行降采样,最大池化就是在图片中用每个区域的最大值代表这个区域,平均池化就是用每个区域平均值代表这个区域。

卷积神经网络反向传播推导
池化层反向传播
池化层的反向传播比较容易理解,我们以最大池化举例,上图中,池化后的数字6对应于池化前的红色区域,实际上只有红色区域中最大值数字6对池化后的结果有影响,权重为1,而其它的数字对池化后的结果影响都为0。假设池化后数字6的位置delta误差为 \delta ,误差反向传播回去时,红色区域中最大值对应的位置delta误差即等于 \delta ,而其它3个位置对应的delta误差为0。
因此,在卷积神经网络最大池化前向传播时,不仅要记录区域的最大值,同时也要记录下来区域最大值的位置,方便delta误差的反向传播。
而平均池化就更简单了,由于平均池化时,区域中每个值对池化后结果贡献的权重都为区域大小的倒数,所以delta误差反向传播回来时,在区域每个位置的delta误差都为池化后delta误差除以区域的大小。
卷积层反向传播
虽然卷积神经网络的卷积运算是一个三维张量的图片和一个四维张量的卷积核进行卷积运算,但最核心的计算只涉及二维卷积,因此我们先从二维的卷积运算来进行分析:

如上图所示,我们求原图A处的delta误差,就先分析,它在前向传播中影响了下一层的哪些结点。显然,它只对结点C有一个权重为B的影响,对卷积结果中的其它结点没有任何影响。因此A的delta误差应该等于C点的delta误差乘上权重B。

我们现在将原图A点位置移动一下,再看看变换位置后A点的delta误差是多少,同样先分析它前向传播影响了卷积结果的哪些结点。经过分析,A点以权重C影响了卷积结果的D点,以权重B影响了卷积结果的E点。那它的delta误差就等于D点delta误差乘上C加上E点的delta误差乘上B。
大家可以尝试用相同的方法去分析原图中其它结点的delta误差,结果会发现,原图的delta误差,等于卷积结果的delta误差经过零填充后,与卷积核旋转180度后的卷积。如下图所示:

好了,直观上的理解有了,我们接下来用数学公式来对此进行证明,尽管它们会有些枯燥:
让我们回顾一下delta误差的定义,是损失函数对于当前层未激活输出 z^l 的导数,我们现在考虑的是二维卷积,因此,每一层的delta误差是一个二维的矩阵。 \delta^l(x,y) 表示的是第l层坐标为(x,y)处的delta误差。假设我们已经知道第l+1层的delta误差,利用求导的链式法则,可以很容易写出下式:
\delta^l(x,y) = \frac {\partial C}{\partial z^l(x,y)}=\sum\limits_{x'}\sum\limits_{y'}\frac {\partial C}{\partial z^{l+1}(x',y')}\frac {\partial z^{l+1}(x',y')}{\partial z^l(x,y)} =\sum\limits_{x'}\sum\limits_{y'}\delta^{l+1}(x',y')\frac {\partial z^{l+1}(x',y')}{\partial z^l(x,y)}
在这里,坐标(x',y')是第l+1层中在前向传播中受第l层坐标(x,y)影响到的点,它们不止一个,我们需要将它们加起来。再利用前向传播的关系式:
z^{l+1}(x',y')={\sum\limits_a\sum\limits_b}\sigma(z^l(x'+a,y'+b))w(a,b)+b^{l+1}
我们可以进一步将表达式展开:
\delta^l(x,y) =\sum\limits_{x'}\sum\limits_{y'}\delta^{l+1}(x',y')\frac {\partial{\sum\limits_a\sum\limits_b}\sigma(z^l(x'+a,y'+b))w(a,b)+b^{l+1}}{\partial z^l(x,y)}
后面一大串尽管看起来很复杂,但实际上很容易就可以简化:
\delta^l(x,y) =\sum\limits_{x'}\sum\limits_{y'}\delta^{l+1}(x',y') w(a,b)\sigma'(z^l(x,y))
同时我们得到两个限制条件 x'+a=x 和 y'+b=y
将限制条件代入上式可得:
\delta^l(x,y) =\sum\limits_{a}\sum\limits_{b}\delta^{l+1}(x-a,y-b) w(a,b)\sigma'(z^l(x,y))
再令 a'=-a 以及 b'=-b
\delta^l(x,y) =\sum\limits_{a'}\sum\limits_{b'}\delta^{l+1}(x+a',y+b') w(-a',-b')\sigma'(z^l(x,y))
我们最终的结论得到了:
\delta^l =\delta^{l+1}* ROT180(w^{l+1})\odot\sigma'(z^l)
我们可以短暂的庆祝一下子了,然而我们目前的结论还只是基于二维卷积,我们还需要把它推广到我们卷积神经网络中张量的卷积中去。
再回顾一下张量的卷积,后一层的每个通道都是由前一层的各个通道经过卷积再求和得到的。
等等,这个关系听起来好像有点熟悉,如果把通道变成结点,把卷积变成乘上权重,这个是不是和全连接神经网络有些类似呢?
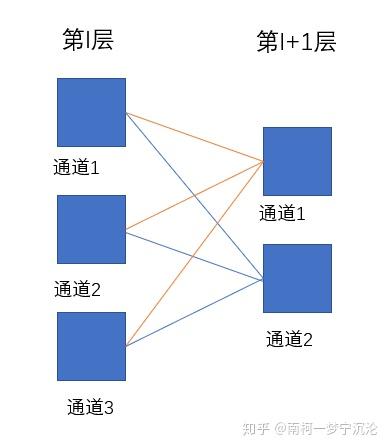
上图中每根连线都代表与一个二维卷积核的卷积操作,假设第l层深度为3,第l+1层深度为2,卷积核的维度就应该为2×filter_size×filter_size×3。第l层的通道1通过卷积影响了第l+1层的通道1和通道2,那么求第l层通道1的delta误差时,就应该根据求得的二维卷积的delta误差传播方式,将第l+1层通道1和通道2的delta误差传播到第l层的delta误差进行简单求和即可。
已知第l层delta误差,求该层的参数的导数 \frac{\partial C}{\partial w^l}
\delta^l = \frac{\partial C}{\partial z^l} , z^l = a^{l-1}*w^l+b^l
第l层卷积核 w^l 是一个4维张量,它的维度表示为卷积核个数×行数×列数×通道数。实际上,可以把它视为有卷积核个数×通道数个二维卷积核,每个都对应输入图像的对应通道和输出图像的对应通道,每一个二维卷积核只涉及到一次二维卷积运算。那求得整个卷积核的导数,只需分析卷积核数×通道数次二维卷积中每个二维卷积核的导数,再将其组合成4维张量即可。
所以我们分析二维卷积即可:

可以利用之前的分析方法,卷积核上点A显然对卷积结果每一个点都有影响。它对卷积结果的影响等于将整个原图左上3×3的部分乘上点A的值,因此delta误差反向传播回时,点A的导数等于卷积结果的delta误差与原图左上3×3红色部分逐点相乘后求和。因此二维卷积核的导数等于原图对应通道与卷积结果对应通道的delta误差直接进行卷积。
\frac {\partial C}{\partial w^l} = \frac {\partial C}{\partial z^l} \frac{\partial z^l}{\partial w^l}= \delta^l * a^{l-1}
我们将原图通道数×卷积结果通道数个二维卷积核的导数重新进行组合成4为张量,即可得到整个卷积核的导数。
下面我们从数学公式进行推导:
\frac {\partial C}{\partial w^l(a,b)}= \sum\limits_x\sum\limits_y \delta^l(x,y) \frac{\partial z^l(x,y)}{\partial w^l(a,b)}
\frac {\partial C}{\partial w^l(a,b)}= \sum\limits_x\sum\limits_y \delta^l(x,y) \frac{\partial \sum\limits_{a'}\sum\limits_{b'}\sigma(z^{l-1}(x+a',y+b'))w^l(a',b')+b^l} {\partial w^l(a,b)}
同样我们可以进行简化,并得到两个限制条件: a'=a 和 b'=b :
\frac {\partial C}{\partial w^l(a,b)}= \sum\limits_x\sum\limits_y \delta^l(x,y) \sigma(z^{l-1}(x+a,y+b)) \sigma'(z^{l-1}(x+a,y+b))
\frac {\partial C}{\partial w^l}= \delta^l*\sigma(z^{l-1})
这一次我们并不需要进行旋转180度这种操作。
已知第l层delta误差,求该层的参数的导数 \frac{\partial C}{\partial b^l}
我们的 b^l 是一个列向量,它给卷积结果的每一个通道都加上同一个标量。因此,在反向传播时,它的导数等于卷积结果的delta误差在每一个通道上将所有delta误差进行求和的结果。
\frac{\partial C}{\partial b^l}=\frac{\partial C}{\partial{z^l}} \frac{\partial z^l}{\partial b^l}=\sum\limits_{x}\sum\limits_{y}\delta^l
提供简单的公式证明如下:
\frac{\partial C}{\partial b^l} = \sum\limits_x \sum\limits_y \frac {\partial C}{\partial z^l(x,y)} \frac{\partial z^l(x,y)}{\partial b^l} 由于 \frac{\partial z^l(x,y)}{\partial b^l} 为1
所以:
\frac{\partial C}{\partial b^l} = \sum\limits_x \sum\limits_y \delta^l 得证
卷积神经网络包括卷积层,池化层和全连接层,本文介绍了卷积层和池化层的反向传播算法以及各层参数导数的计算方法,全连接层的反向传播方法以及参数导数的计算在之前文章中也介绍过了。
让我们对卷积神经网络的训练过程进行一个总结:
- 对神经网络进行初始化,定义好网络结构,设定好激活函数,对卷积层的卷积核W、偏置b进行随机初试化,对全连接层的权重矩阵W和偏置b进行随机初始化。
设置好训练的最大迭代次数,每个训练batch的大小,学习率 \eta - 从训练数据中取出一个batch的数据
- 从该batch数据中取出一个数据,包括输入x以及对应的正确标注y
- 将输入x送入神经网络的输入端,得到神经网络各层输出参数z^l和a^l
- 根据神经网络的输出和标注值y计算神经网络的损失函数
- 计算损失函数对输出层的delta误差\delta^L
- 利用相邻层之间delta误差的递推公式求得每一层的delta误差
如果是全连接层δ^l=(W^{l+1} )^T δ^{l+1}⊙σ' (z^l)
如果是卷积层 \delta^l =\delta^{l+1}* ROT180(w^{l+1})\odot\sigma'(z^l)
如果是池化层 \delta^l = upsample(\delta^{l+1})\odot\sigma'(z^l) - 利用每一层的delta误差求出损失函数对该层参数的导数
如果是全连接层:
\frac{∂C}{∂W^l }=δ^l (a^{l-1} )^T ,\frac{∂C}{∂b^l }=δ^l
如果是卷积层:
\frac {\partial C}{\partial w^l}= \delta^l*\sigma(z^{l-1}) , \frac{\partial C}{\partial b^l} = \sum\limits_x \sum\limits_y \delta^l - 将求得的导数加到该batch数据求得的导数之和上(初始化为0),跳转到步骤3,直到该batch数据都训练完毕
- 利用一个batch数据求得的导数之和,根据梯度下降法对参数进行更新
W^l=W^l-\frac{η}{batch\_size} \sum\frac{∂C}{∂W^l }
b^l=b^l-\frac{η}{batch\_size} \sum \frac{∂C}{∂b^l } - 跳转到步骤2,直到达到指定的迭代次数
在下一篇文章,我将带领大家利用这些理论知识,使用Python从底层实现一个简单但经典的卷积神经网络——LeNet,并用它完成手写数字识别任务。
参考:
[1]刘建平Pinard:卷积神经网络(CNN)反向传播算法
[2]Grzegorz Gwardys:Convolutional Neural Networks backpropagation: from intuition to derivation
[3]Kunlun Bai:A Comprehensive Introduction to Different Types of Convolutions in Deep Learning
[4]CS231n Convolutional Neural Networks for Visual Recognition
