RNA Velocity and Beyond 系列[2] - Model
本文使用 Zhihu On VSCode 创作并发布
时隔许久再次更新,本来想一口气写完模型部分还有参数估计部分,但是发现参数估计部分有点长,所以拆开写了。
本文主要参考李铁军老师挂在 biorxiv 上的文章:
本文首先描述这个过程的模型(也就是如果知道那些 参数的情况下,mRNA 应该是怎么样的),然后说明怎么从已有的表达谱数据中估计这些参数。(本文只有最简单的利用 steady state 来估计) 这篇文章只讨论了确定性模型,没有从化学主方程的那种角度讨论,大概就相当于没有考虑这个离散性,不需要使用随机微分方程来刻画。建议对这部分感兴趣的读者可以自行看李铁军老师的文章。 没看过前文的可以考虑先看前文 RNA Velocity and Beyond 系列[1] - Introduction
Model
Deterministic Model
首先根据 RNA velocity 的 dynamics 可以得到相对应的 ODE
\begin{array}{l} \frac{\mathrm{d} u}{\mathrm{~d} t}=\alpha(t)-\beta u(t) \\ \frac{\mathrm{d} s}{\mathrm{~d} t}=\beta u(t)-\gamma s(t) \end{array}
对于转录本的生成过程我们可以知道,对于 \alpha,我们有
\alpha(t)=\left\{\begin{array}{ll} \alpha^{\text {on }}, & t \leq t_{s} \\ \alpha^{\text {off }}=0, & t>t_{s} \end{array}\right.
这个式子代表当转录启动的之后,转录的速率是一个常数 \alpha^{on},反之当转录关闭的时候,生成速率为 0。
而我们认为的 RNA velocity 也就是 spliced mRNA 的变化速度为
\boldsymbol{v}(t)=\left(v_{g}(t)\right)_{g}=\left(\frac{\mathrm{d} s_{g}}{\mathrm{~d} t}\right)_{g}=\left(\beta_{g} u_{g}(t)-\gamma_{g} s_{g}(t)\right)_{g} \in \mathbb{R}^{n_{g}}
在这个式子中其实已经做了 \alpha, \beta, \gamma 都是常数的假设,在这些假设的前提下,我们可以对上述方程求得显式解。
Case 1 \beta \neq \gamma
解上述方程可以得到
\begin{aligned} u(t) &=u_{0} e^{-\beta t}+\frac{\alpha}{\beta}\left(1-e^{-\beta t}\right) \\ s(t) &=s_{0} e^{-\gamma t}+\frac{\alpha}{\gamma}\left(1-e^{-\gamma t}\right)+\frac{\alpha-\beta u_{0}}{\gamma-\beta}\left(e^{-\gamma t}-e^{-\beta t}\right) \end{aligned}
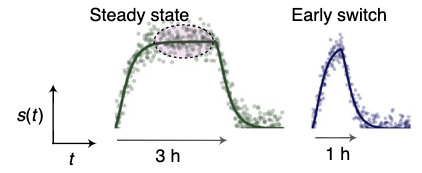
但是值得注意的是,上式代表的是一个 stage,如果 switch time t_s 刚好被包含在这段计算的时间内,那么就需要分开处理,分阶段得到。 具体见下图也就是右边部分。
分阶段
对于第一阶段 t \leq t_s ,如果假设 (u_0, s_0) = (0,0) ,我们可以用 上述的显式解写得
\begin{aligned} u(t) &=\frac{\alpha}{\beta}\left(1-e^{-\beta t}\right) \\ s(t) &=\frac{\alpha}{\gamma}\left(1-e^{-\gamma t}\right)+\frac{\alpha}{\gamma-\beta}\left(e^{-\gamma t}-e^{-\beta t}\right) \\ \end{aligned}
而对于 第二个阶段也就是 t_s \leq t 时,我们不妨定义 \left(u_{s}, s_{s}\right):=\left(u\left(t_{s}\right), s\left(t_{s}\right)\right),那么在接下来的 off 阶段我们有
\begin{aligned} u(t) &=u_{s} e^{-\beta\left(t-t_{s}\right)} \\ s(t) &=s_{s} e^{-\gamma\left(t-t_{s}\right)}-\frac{\beta u_{s}}{\gamma-\beta}\left(e^{-\gamma\left(t-t_{s}\right)}-e^{-\beta\left(t-t_{s}\right)}\right) \end{aligned}
换句话就是两次利用方程的解析解,因为这个过程是被分成了两部分。
Case 2: \beta = \gamma
和之前的区别大概就只是数值求解上的区别。所以对于 on stage 的解就是
\begin{aligned} u(t) &=u_{0} e^{-\beta t}+\frac{\alpha}{\beta}\left(1-e^{-\beta t}\right) \\ s(t) &=s_{0} e^{-\beta t}+\frac{\alpha}{\beta}\left(1-e^{-\beta t}\right)-\left(\alpha-\beta u_{0}\right) t e^{-\beta t}\\ \end{aligned}
其中 t \leq t_s,如果此时 (u_0, s_0) = (0,0) 可以得到这段时间的解为
\begin{aligned} u(t) &=\frac{\alpha}{\beta}\left(1-e^{-\beta t}\right) \\ s(t) &=\frac{\alpha}{\beta}\left(1-e^{-\beta t}\right)-\alpha t e^{-\beta t} \end{aligned}
而在 off stage 可以得到
\begin{aligned} u(t) &=u_{s} e^{-\beta\left(t-t_{x}\right)} \\ s(t) &=s_{s} e^{-\beta\left(t-t_{s}\right)}+u_{s} \beta t e^{-\beta\left(t-t_{s}\right)} \end{aligned}
而且其实也可以从之前的 \beta \neq \gamma 的式子取极限得到。
Inference of RNA velocity
有了上面的模型,那么下一步就是通过数据来拟合这些参数。t_s, \alpha,\beta, \gamma。
从总体来说,我们可以知道 t_s, (u_s, S_s) (表示 switch time,switch 之后的状态)是无法从观测数据得到的,是 hidden variable,所以需要 EM 算法来求解。
Steady State Model
先从最简单的开始,如果我们认为 on stage 足够久的话,我们可以认为最后的状态是 steady state ,因此可以得到 steady state 的等式为
\frac{\mathrm{d} s}{\mathrm{~d} t}=\beta u(t)-\gamma s(t)=0
而通过这个式子可以得到可以通过最小二乘法线性拟合来估计参数:
\nu^{*}=\left(\frac{\gamma}{\beta}\right)^{*}=\underset{\nu}{\arg \min } \beta^{2}\|\boldsymbol{u}-\nu \boldsymbol{s}\|^{2}=\frac{\boldsymbol{u}^{\mathrm{T}} \boldsymbol{s}}{\|\boldsymbol{s}\|^{2}}
最后一个等式假设 \beta =1(不失一般性的假设,也可以看做无量纲化,得到的相对值,这个假设也是开始的 Velocity 原文使用的) 据此可以得到 v 的估计。
\boldsymbol{v}=\left(v_{g}\right)_{g}, \quad v_{g}=u_{g}-\nu_{g}^{*} s_{g}
值得说明的是,在做回归估计的时候需要利用那些处在 steady state 的细胞(在 velocity 原文中也就是 那个 extreme 假设,只取 u,v 图中两端的 cells)。
基于 v_{g}=u_{g}-\nu_{g}^{*} s_{g} 其实可以发现 velocity 的值其实就是 u, s 的一个线性组合,所以在这个情况下可能不能提供太多新的信息。
EM algorithm for the transient models
前面一小节似乎已经可以估计出参数了,但是为什么还要用 EM 算法呢? 这是因为之前的 Steady state 的假设是不一定满足的,或者换言之,上一小节的估计需要找到那些已经处于 steady state 的细胞。(并不一定能在数据中找到,而且换言之就只利用了一部分数据来估计参数,那么自然就可能比较 sensitive)。
而利用 EM 算法来估计的原因是我们可以观测到的数据 (u,s) 中无法知道一些hidden variable t_s, (u_s, s_s),对于每个 细胞和 每个 gene。 如果直接使用 MLE 之类的优化参数不现实。
因此采用 EM 算法迭代的优化。
大致的核心思想在于,首先随机初始化参数,然后借助参数可以得到对隐变量的估计,虽然再根据估计出的隐变量来重新估计参数,循环往复,左脚踩右脚逐渐上天hhh,但是需要说明的就是,如何重新估计参数是有讲究的,这一步保证了更新的 log-likelihood 是不减的。但也要注意的就是 EM 算法不保证能找到全局最优,因为 log likelihood 不减这个性质只能保证找到一个局部最优解。
未完待续,具体 EM 估计参数的细节见下文~