优化算法之指数移动加权平均

1.前言

(1)加权平均VS算术平均

• 算术平均数的定义：一般地，对于 n 个数 x_{1},x_{2},x_{3},...,x_{n} 我们把 \frac{1}{n}(x_{1}+x_{2}+x_{3}+...+x_{n}) 叫做这 n 个数的算术平均数，简称平均数记作 \bar{x} ，读作 x 拔。
• 加权平均数：在实际问题中，一组数据里的各个数据的重要程度未必相同。因而，在计算这组数据的时候，往往给每个数据一个权。加权平均数一般来说，如果在 n 个数中， x_{1}出现的 f_{1} 次， x_{2} 出现 f_{2} 次，...， x_{k} 出现 f_{k} 次 (f_{1}+f_{2}+f_{3}+...+f_{k}=n) ，则 \bar{x}=\frac{1}{n}(x_{1}f_{1}+x_{2}f_{2}+x_{3}f_{3}+x_{k}f_{k}) 其中 f_{1},f_{2},f_{3}...f_{k} 叫做权。(权越大对平均数的影响也就越大)
• 算术平均数与加权平均数有什么区别?算术平均数是加权平均数的一种特殊情况(他特殊在各项的权相等为1)；在实际问题中，各项权不相等的时，计算平均数时就要采用加权平均数，当各项权相等时，计算平均数就要采用算术平均数。
• 加权平均数中的权有(1)整数的形式；(2)比的形式；(3)百分比的形式；

例子：

整数的形式其实很好理解就是出现的频数。

其实这个例子的权重是股票占总股票的比重。也就是权重是一个比的形式。

(2)加权平均法VS移动平均法

• 移动平均法是用一组最近的实际数据来预测未来一期或几期内的预测数一种常用方法。移动平均法适用于即期预测。当产品需求既不增长也不快速下降，且不存在在季节性因素时，移动平均法能有效地消除预测中的随机波动，是非常有用的。移动平均法根据预测时使用的各元素的权重不同，可以分为：简单移动平均(一次移动平均法和二次移动平均法)和加权移动平均。

1.简单的移动平均法

(一次移动平均法)是收集一组观察值，计算这组观察值的均值，利用这个均值作为下一期的预测值。在移动平均值的计算中包括的过去观察值的实际个数，必须一开始就明确规定。每出现一个新的观察值，就要从移动平均中减去一个最早的观察值，再加上一个最新的观察值，计算移动平均值，这一新的移动平均值就最为下一期的预测值。

• 移动平均法有两种极端情况:(1)在移动平均值的计算中包括的过去观察值的实际个数 N=1 ，这时利用最新的观察值作为下一期的预测值；(2) N=n ，这时利用全部的 n 个观察值的算术平均值作为预测值。
• 当数据的随机因素较大的时候，宜选用较大的 n ，这样有利于较大的限度地平滑由随机性所带来的严重偏差；反之，当数据的随机因素较小的时候，宜选用较小的 n ，这有利于跟踪数据的变化，并且预测值滞后的期数也少。
• 设时间序列 x_{1},x_{2},x_{3},..., 移动平均法可以表示 F_{t+1}=\frac{(x_{t}+x_{t-1}+x_{t-2}+...+x_{t-N+1})}{N}=\frac{1}{N}\sum_{t-N+1}^{t}{x_{i}} 式子中： x_{t} 为最新观察值； F_{t+1} 为下一期预测值；由移动平均法计算公式可以看出，每一新预测值是对前一移动平均预测值的修正， n 越大平滑效果愈好。
• 移动平均法的优点：计算量少 ；移动平均线能较好的反应时间序列的趋势以及变化
• 移动平均法的两个主要限制：计算移动平均必须具有 n 个过去观察值，当需要预测大量的数值时，就必须存储大量数据； n个过去观察值中每一个权数都相等，而早于 (t-N+1) 期的观察值的权数等于0，而实际上往往是最新观察值包含更多信息，因具有更大的权重。

2.加权移动平均法

加权移动平均给固定跨越期限内的每个变量值以相等的权重。其原理是：历史各期产品需求的数据信息对预测未来期内的需求量的作用是不一样的。除了以 n 为周期性变化外，远离目标期的变量值的影响力相对较低，故应给予较低的权重。

• 加权移动平均法的计算公式： F_{t}=w_{1}A_{t-1}+w_{2}A_{t-2}+w_{3}A_{t-3}+...+w_{n}A_{t-n} 其中式子中的 w_{1} 是 t-1 期实际销售额的权重； w_{2} 是第 t-2 期实际销售额的权重； w_{n} 是第 t-n 期实际销售额的权重； n 为预测时期数； w_{1}+w_{2}+w_{3}+...+w_{n}=1 。
• 在运用加权平均时，权重的选择是一个应该注意的问题，经验法和试算法使选择权重最简单的方法。一般而言，最近期的数据最能预测未来的情况。因而权重应大一些。例如，根据前一个月的利润和生产能力比起根据前几个月能更好的估计下一个月的利润和生产能力。但是，如果数据时季节性的，则权重也应该是季节性的。
• 使用移动平均法能预测能平滑掉需求的突然波动对预测结果的影响。但移动平均法运用时也存在着如下的问题：
• 加大移动平均法的期数(就是 n )会使平滑波动效果更好，但会使预测值对数据实际变动更不敏感。(也就是图像会往右移动，有时延)
• 移动平均值并不能总是很好的反应出趋势。由于是平均值，预测值总是停留在过去的水平上而无法预计会导致将来更高或更低的波动。
• 移动平均法要大量的过去数据记录
• 它哦引进愈来愈期的新数据，不断修改平均值。以之作为预测值。
• 移动平均法的基本原理：是通过移动平均消除时间序列中的不规则变动和其他变动，从而揭示出时间序列的长期趋势。

补充：

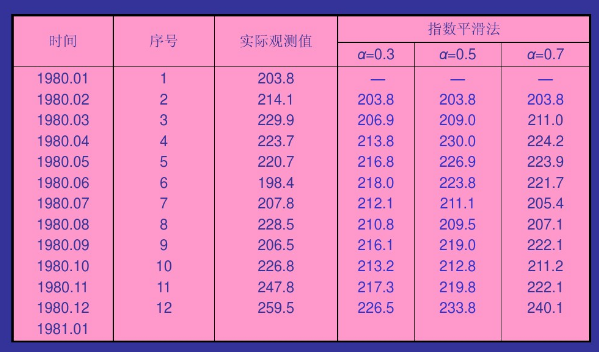
指数平滑法是对加权移动平均法的改进，它是将前期预测值和前期实际值分别确定不同的权数(二者权数和为1)。只需要三个数据，所有预测方法中，指数平滑法采用较多，常用语短期预测。选择合适的 \alpha 值。实际需求稳定，选取较小的 \alpha 值，反之选取较大的 \alpha 值。指数平滑法有很多种，有一次指数平滑预测、二次指数平滑预测以及三次指数平滑预测。我们这里这说一次指数平滑预测。

• 一次指数平滑预测是利用前一期的预测值 F_{t} 代替 x_{t-n} 得到预测的通式，即： F_{t+1}=\alpha x_{t}+(1-\alpha)F_{t}
• 由一次指数平滑法的通式可见：一次指数平滑法是一种加权预测，权数为 \alpha 。它既不需要存储全部的历史数据，也不需要存储一组数据，从而可以大大减少数据存储问题，甚至有时只需一个最新观察值、最新预测值和 \alpha 值，就可以进行预测。它提供的预测值是前一期预测值加上前期预测值中的误差的修正值。
• 一次指数平滑法的初始值的确定有几种方法：(1)取第一期的实际值为初值；(2)取最初几期的平均值为初值。一次指数平滑法比较简单，但也有问题。问题之一便是力图找到最佳的 \alpha 值，以使均方差最小，这需要通过反复试验确定。

2.指数加权移动平均

说了这么多那什么是指数加权移动平均呢？其实他也是加权移动平均的一种改进。指数加权移动平均(Exponentially Weighted Moving Average)，他是一种常用的序列处理方式。在 t 时刻，他的移动平均值公式是： V_{t}=\beta V_{t-1}+(1-\beta)\theta_{t} t=1,2,3,...n ，其中 V_{t} 是 t 时刻的移动平均预测值； \theta_{t} 为 t 时刻的真实值； \beta 是权重；其实这个和上面的指数平滑预测很是相像。但是有有所不同，指数滑动平均 F_{t+1}=\alpha x_{t}+(1-\alpha)F_{t} 是通过当前 t 时间的真实值和 t 时间的预测值来进行估计预测下一个时期。而我们所说的指数加权移动平均就是通过当前的实际值和前一段时期(由 \beta 约定平均了多少以前的数据)来进行平滑修改当前的值，来生成一个平稳的趋势曲线。

物理意义：系数 \beta 越小就说明对过去测量值的权重越低，也就是对当前抽样值的权重越高。这个时候移动平均估计值的时效性就越强(其实也就是更加拟合点分布的趋势)。反之，则会越弱。指数移动加权平均还有另一个特点就是能吸收瞬时突发的能力也就是平稳性(使得得到的曲线趋势能够更加平缓)，如果对过去估计值的权重越低也就是 \beta 越小，那么他的平稳性就差一点，反之平稳性会增强。

举一个例子：

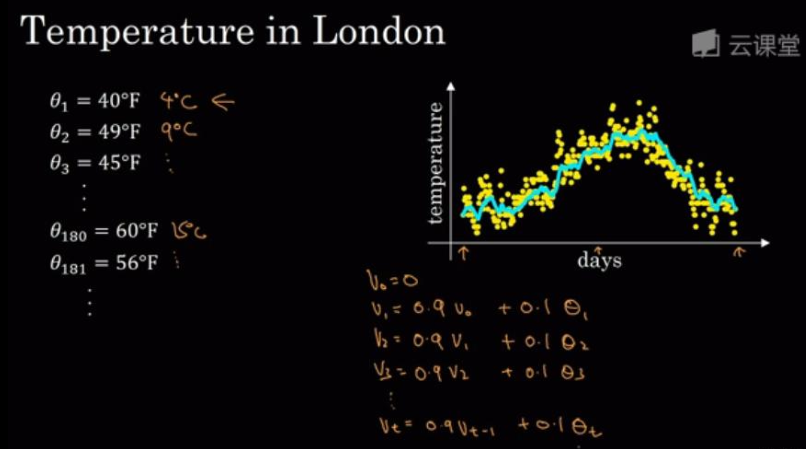
其实这里的曲线就是当 v_{0}=0 作为移动平均的初始值，然后将对应的实际的温度值带入递归式子中，然后得出的曲线。其实从上面也可以看出来 \beta 的选择尤为的重要。这个温度的例子，吴恩达老师选择了 0.9 作为 \beta 的值。可以看出曲线要平坦一点，这是因为你平均了几天的温度，所以这个曲线波动更小，更加平坦，缺点就是曲线会失去时效性，在图中的表现就是曲线会向右移动，那因为现在要平均的温度值更多，要平均更多的值，指数加权平均公式在温度变化的时，能更加适应缓慢一些，所以会出现一定的延迟。

• \beta=0.98 的时候，曲线会更加平缓(稳定性高)，但是趋势曲线会向右移动(时效性差)
• \beta=0.5 的时候，由于只平均了两天的温度，平均的数据太少了，得到的曲线会有更多的噪声也就是(稳定性差)更有可能出现异常值，但是趋势曲线能够更加适应拟合你的原始数据，也就是趋势曲线的(时效性高)

通过上面两个极端值可以看出，我们可以选择一个合适的 \beta 值来使曲线既平缓又不偏离数据点。也就是不会有太多的噪声同时也不会向右偏离太多。 \beta 是一个很重要的参数，可以取得稍微不同的效果，往往中间某个值效果最好。那我们说为什么知道 \beta 值就知道他平均了多少天呢？

3.指数移动加权平均的理解

我们使用 \beta=0.9 来看看指数移动加权平均的原理是什么?

V_{100}=0.9V_{99}+0.1\theta_{100}

V_{99}=0.9V_{98}+0.1\theta_{99}

V_{98}=0.9V_{97}+0.1\theta_{98}

...

我们将式子一步一步的带入得到最终式子： V_{100}=0.1\theta_{100}+0.1*0.9\theta_{99}+0.1*0.9*0.9\theta_{98}+...+0.1*0.9^{99}\theta_{1} 通过式子我们可以很清楚的看出对于求的 V_{100} 的值，可以看做是 \theta_{1}\rightarrow \theta_{100} 的温度值与对应的指数衰减函数对应项相乘之后在求和。

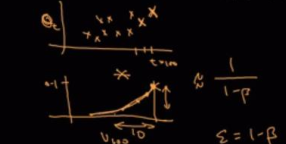
我们上回看到当 \beta=0.5 的时候我们说平均了两天，我们发现 0.5^{2}\approx\frac{1}{e}\approx 0.35 再去乘于 0.5 那么可以看出后面的数也会很小，所以我们再去考虑。同理， \beta=0.9的时候，0.9^{10}\approx \frac{1}{e}\approx0.35 也就说平均了10天。 \frac{1}{e}*0.1 我们认为这个值就已经很小了，所以不再去考虑后面的数据了，所以说当 \beta=0.9 的时候只平均了 10 天的数据。

优势：

V 是用来计算数据的指数加权平均数，计算指数加权平均数只占单行数字的存储和内存，

当然并不是最好的，也不是最精准的计算平均数的方法，如果你需要计算时间窗，你可以直

接过去 10 天的总和或者过去 50 天的总和除以 10 或 50 就好了，如此往往会得到更好的估

测，但缺点是如果保存最近的气温和过去 10 天的总和，必须占更多的内存，执行更加复杂，

而计算指数加权平均数只占单行数字的存储和内存。他的效率和资源的占有率会大大的减小。 所以在机器学习中大部分采用指数加权平均的方法计算平均值。

4.指数加权移动平均的偏差修正

当我们取 \beta=0.98 的时候，实际上我们得到的并不是绿色的曲线而是紫色的曲线，通过紫色曲线我们看出在预测的初期值和我的真实值的差距很大，所以引入了偏差修正的概念。

• 还是上面温度的例子我们 V_{0}=0 ， \theta_{1}=40 那么通过指数移动加权平均的公式可以得到 V_{1}=0.98V_{0}+0.02\theta_{1}=0.98*0+0.02*40=8 那可以看出算出的 V_{1}=8 和实际 \theta_{1} 的 40 相比差距还是不小的。 V_{2}=0.98V_{1}+0.02\theta_{2}=0.0196*\theta_{1}+0.02*\theta_{2} 同理 V_{2} 也要远远小于 1 号和 2 号数据。所以可以看出 V_{1} ...这样的前期移动平均值并不能很好的估测温度。
• 引入偏差就是为了解决估测初期预测不准确的问题。那么如何去做呢？
• 指数加权平均公式： V_{t}=\beta V_{t-1}+(1-\beta)\theta_{t}
• 带修正偏差的指数加权平均公式： V_{t}^{'}=\frac{V_{t}}{1-\beta^{t}}=\frac{(\beta V_{t-1}+(1-\beta)\theta_t)}{1-\beta^{t}}
• 当 t=2 的时候， 1-\beta^{2}=1-(0.98)^2=0.0396 , V_{2}^{'}=\frac{V_{2}}{1-\beta^{2}}=\frac{0.0196*\theta_{1}+0.02*\theta_{2}}{0.0396} ，可以看出比原来的效果好了很多。对于 1-\beta^{t} 我们可以看出，随着 t 的逐渐增大， \beta^{t} 会逐渐接近与0，那么 1-\beta^{t} 就会逐渐接近与 1 ，那么我们从公式上可以看出，我们的偏差修正最终会变成(如果数据多的话) V^{'}_{t}=V_{t} ，公式最终会变成V^{'}_{t}=V_{t}=\beta V_{t-1}+(1-\beta)\theta_{t}。所以在机器学习中，在计算指数加权平均数的大部分时候，大家不太在乎偏差修正，大部分宁愿熬过初始阶段，拿到具有偏差的估测，然后继续计算下去。如果你关心初始时期的偏差，修正偏差能帮助你在早期获得更好的估测。