矩阵与数值计算(2)——矩阵三角分解LU、PALU、Cholesky三角分解、QR分解
前言
矩阵分解是设计算法的主要技巧,通过分解可以将复杂问题转化为几个简单问题求解,通常完成这一转化任务的主要技巧就是矩阵分解。例如,我们知道上三角矩阵和下三角矩阵是容易求解的,或者对角矩阵是最理想的求解形式,我们通过矩阵的分解去将原本的复杂问题,转化为若干个易于求解的矩阵来运算。
一、高斯消去法与LU分解
大学本科期间学校讲授的线性代数课程,关于Ax=b这类矩阵求解方式采用的是高斯消去法的方式(与高中阶段的多元一次方程求解方式一样)。而为我们矩阵分解打头阵的分解形式就是LU分解,那么这两种分解有什么区别呢?首先我们从这两种方法的计算复杂度角度逐渐切入问题的核心。
我们这里默认你掌握线性代数的基本知识,那么高斯消去法的计算过程我们可以通过下面这个图片来进行概括。

如果有这样一个问题

我们通过高斯消元法,最后会得到一个这样的等价问题,

这个高斯消去的过程如果写成矩阵相乘的过程,那么就如下所示,

通过上图我们就得到了LU分解的基本形式,通过三个L矩阵对A进行行变换我们得到一个上三角矩阵,通过这个上三角矩阵U和三个行变换矩阵的乘积L,就得到了LU分解的定义。

定义
对于n阶方阵A,如果存在n阶单位下三角矩阵L和n阶上三角形矩阵U,使得A=LU,则称其为矩阵A的LU分解,也称为Doolittle分解。
对于Gauss消去法和LU分解法的乘法计算计算量都是在 \frac{n^3}{3} 量级,这个就是分解过程的乘法计算量,推导过程可以模拟一下高斯消去法的整体过程,就可以得到如下的等式,

详细推导过程不要求掌握,但是可以通过阅读教材或者参考资料的详细推导来了解这个过程。需要记住的是,分解过程始终是 \frac{n^3}{3} 量级,求解过程是 \frac{n^2}{2} 量级。
那么一个Ax=b的问题,我们就可以转化为LU分解计算,主要分为三步
- A=LU 乘法量级 \frac{n^3}{3}
- Ly=b 乘法量级 \frac{n^2}{2}
- Ux=y 乘法量级 \frac{n^2}{2}
接下来我们通过一道题目来实战一下大家对其理解的如何:

欢迎大家在评论区发表你的看法。
以上我们基本明确了矩阵的LU分解过程。那么任意一个矩阵A的LU分解是否一定存在且唯一的呢?下面我们来分析LU分解的存在唯一性。
由高斯消去法的步骤我们知道,如果想要不断的消去,则要求A在消去过程中的主对角线元素也就是主元 a_{kk}\ne0 ,但是我们现在只能通过高斯法一步步来判断是否可继续执行高斯消去法。有没有更加便捷的方式帮助我们判断矩阵A是否可以进行LU分解呢?
答案是可以。


这样我们就把存在性和唯一性的问题转化为矩阵A的k阶主子式是否等于0的问题。如果A的主子式都不为零,那么矩阵A可以进行LU分解,且该分解唯一。
要注意一点,能进行LU分解的矩阵A,其LU分解不一定唯一。一定要搞清楚与上面定理2.1的区别。
二、Crout分解和LDU分解
LDU分解其实很简单,只需要将LU分解简单变化即可。我们知道U是一个上三角矩阵,我们将其对角元元素提取出来形成一个对角矩阵D,则剩下的新的U和原来的L,其三者就组成了LDU分解。

如果把LD的乘积作为一个矩阵,我们就得到了Crout分解。

例题:通过LU分解求解矩阵的逆。

三、带主元的LU分解
我们知道LU分解,要求主元不为0,假设我们遇到了主元为0的情况,LU分解就没有办法进行下去了。还会涉及误差的问题。LU分解存在的两个问题是:
- 有些有解的问题不能通过LU分解来求解
- 如果某些主元过小,会引入较大的误差。
为了解决这两个问题,想到了选主元策略。每次进行消去操作的时候,我们要挑选一下主元,然后再进行操作。详细来说:
①第k列主元及主元以下元素中挑选绝对值最大的数。
②通过初等变换,使得该数位于主对角线上。
我们取上述相同问题,前两步为例

初等行变换矩阵我们称之为P。这个带选主元的消去法,可以概括成下面的式子。
\begin{align} &L_3P_3L_2P_2L_1P_1A=U\\ &L_3P_3L_2P_3^{-1}P_3P_2L_1P_2^{-1}P_3^{-1}P_3P_2P_1A=U\\ &L_3\widetilde L_2\widetilde L_1(P_3P_2P_1)A=U\\ &PA=LU \end{align}
进而我们得到矩阵列主元LU分解的定义。
定义:对于任意n阶矩阵A,均存在置换矩阵P、单位下三角矩阵L和上三角矩阵U,使得PA=LU(P、L可以不同,分解不唯一)
这里要说明几点:
- 分解不唯一是因为选列主元的时候有可能两个或两个以上元素的绝对值相等,导致P的选取不唯一。
- LU分解不一定存在,但是列主元LU分解一定存在。
- 满足K阶主子式大于零的LU分解必唯一,但列主元LU分解不一定唯一。
四、正定矩阵的Cholesky分解
正定矩阵的所有主子式都大于零,所以满足LU分解的条件,LU分解存在且唯一。假设 A = LD\widetilde U ,那么我们有 A = LD\widetilde U = A^T=\widetilde U^TD^TL^T ,因为LU分解唯一,所以我们有 L=\widetilde U^T,\quad \widetilde U=L^T 。
接着有
A = LU=LD\widetilde U =LDL^T=LD^{\frac{1}{2}}D^{\frac{1}{2}}L^T=\widetilde L\widetilde L^T
上面这个分解 A=\widetilde L\widetilde L^T 就是Cholesky分解。这个分解可以套用公式进行计算。

上面的公式就是Cholesky分解的过程,直接套用公式可以得出分解矩阵,计算的数序以列序为主。
实际考察中,一般掌握三阶矩阵的计算即可,不必记忆公式的详细细节。
求解方程组时,可以将原问题转化为下面三个等式求解。
\begin{align} &A=LL^T\\ &Ly=b\\ &L^Tx=y \end{align}
五、三对角矩阵的三角分解
三对角矩阵是一类特殊的矩阵,这种特殊矩阵的解法也不同于LU分解,这里提供其独特的解法。

分解成形如上图的两个矩阵LU,我们可以通过计算很容易得到l,u,d的值。
计算次序为 u_1\rightarrow l_2\rightarrow u_2\rightarrow l_3\rightarrow u_3...\rightarrow l_n\rightarrow u_n 。
计算公式为:
\begin{cases} d_i = c_i\\ u_1=b_1\\ u_i = b_i-l_ic_{i-1}\\ l_i = a_i/u_{i-1} \end{cases}
上述这种方法被称为追赶法。我们想要使用这种方法求解方程组还需要满足以下条件。

LU分解是解决中小规模、稠密矩阵的最好方法。
五、条件数与方程组的性态
病态和良态
如果线性方程组Ax=b中,A或b的元素的微小变化就会引起方程组的巨大变化,则称方程组为病态方程组,矩阵A称为病态矩阵。
我们非常不希望这样的矩阵存在,那么如何去衡量这种病态程度呢?从相对误差入手进行分析。
假设 A(x+\delta x)=(b+\delta b) ,即右端项扰动,那我们来看看A,b与x相对误差之间的关系。

基于上面的推导,我们得到了条件数的定义,

条件数就可以看作是矩阵A作用下,将b的轻微扰动放大的倍数。因此通过条件数我们可以了解到矩阵A的病态程度。
特别的,二条件数是矩阵A的 A^HA 的最大特征值与最小特征值的比值开根号。

推导过程简单,这里略过。
条件数的性质:
- 非负性
- 非齐次 cond(aA) = cond(A)
- 满足相容性:cond(AB)≤cond(A)cond(B)

接近奇异的矩阵一般是病态矩阵。
系数矩阵和右端项均扰动
即 (A+\delta A)(x+\delta x)=b+\delta b ,同样我们分析x的相对误差有如下推导。

解的余量与相对误差之间的关系
我们称 ||x-\widetilde x|| 为解的误差, ||b-A\widetilde x|| 为解的余量。
我们可以推导他们之间的关系:
b-A\widetilde x = Ax-A\widetilde x\Rightarrow x-\widetilde x = A^{-1}(b-A\widetilde x) 根据矩阵的相容性\Rightarrow ||x-\widetilde x||\le ||A^{-1}||||b-A\widetilde x||
\frac{||x-\widetilde x||}{||x||}\le \frac{||A||\cdot||A^{-1}||\cdot ||b-A\widetilde x||}{||b||} ,类似地我们还可以推出
\frac{||b-A\widetilde x||}{||A||\cdot||A^{-1}||\cdot ||b||}\le \frac{||x-\widetilde x||}{||x||}
于是,有下列结论,

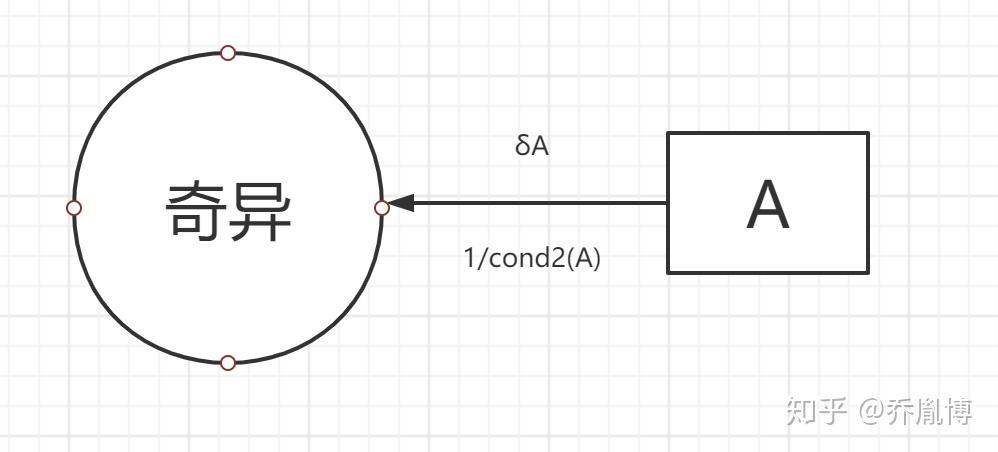
条件数的几何意义,条件数用来刻画矩阵距离奇异的距离。
六、矩阵的QR分解
矩阵的QR分解被评为20世纪十大算法,是所有与矩阵相关算法的底层算法。
QR分解解决的问题是普通分解会导致分解后的条件数增大,我们根据条件数的相容性知道,分解后的条件数要大于等于原矩阵的条件数,为了解决这个问题,我们就用到条件数的第六条性质,关于酉矩阵的性质,于是我们想到通过酉矩阵或许会解决这个问题。
QR分解和LU分解最大的区别就是使用了正交变换来实现矩阵分解。
我们定义QR分解如下,

为了实现QR分解,引入Householder矩阵,Householder矩阵作用到x向量上会将x向量变换到另一个正交的坐标系中,但是变换后的向量y的范数不变,此时x与y关于一个超平面对称,也称为镜面反射。

经过推导我们得到Householder矩阵的求解公式

Householder矩阵的性质

其中第四条性质,是因为求解出来的 \frac{2}{w^Tw}ww^T 矩阵的特征值应该为(2,0,...,0) ,与单位矩阵做减法,得到的特征值为 (-1,1,...,1) 。
总结
上述内容为矩阵三角分解相关的内容,这部分还是需要在题目中不断得到强化和锤炼。接下来将介绍特殊矩阵的特征系统,里面会介绍什么是Schur标准型,为Jordan分解和奇异值分解铺平道路。

