Rosetta基础3: Rosetta能量函数简介
作者: 吴炜坤
此篇为Meiler Lab Rosetta_Energy_Function ppt的解读版本。
一、导读
在Rosetta中评估一个模型的好坏,最直观的方法就是使用Rosetta的打分系统进行评估,也就是常说的能量函数。顾明思议,我们通过一些与能量直接相关的打分项对蛋白质的结构坐标进行打分的过程。
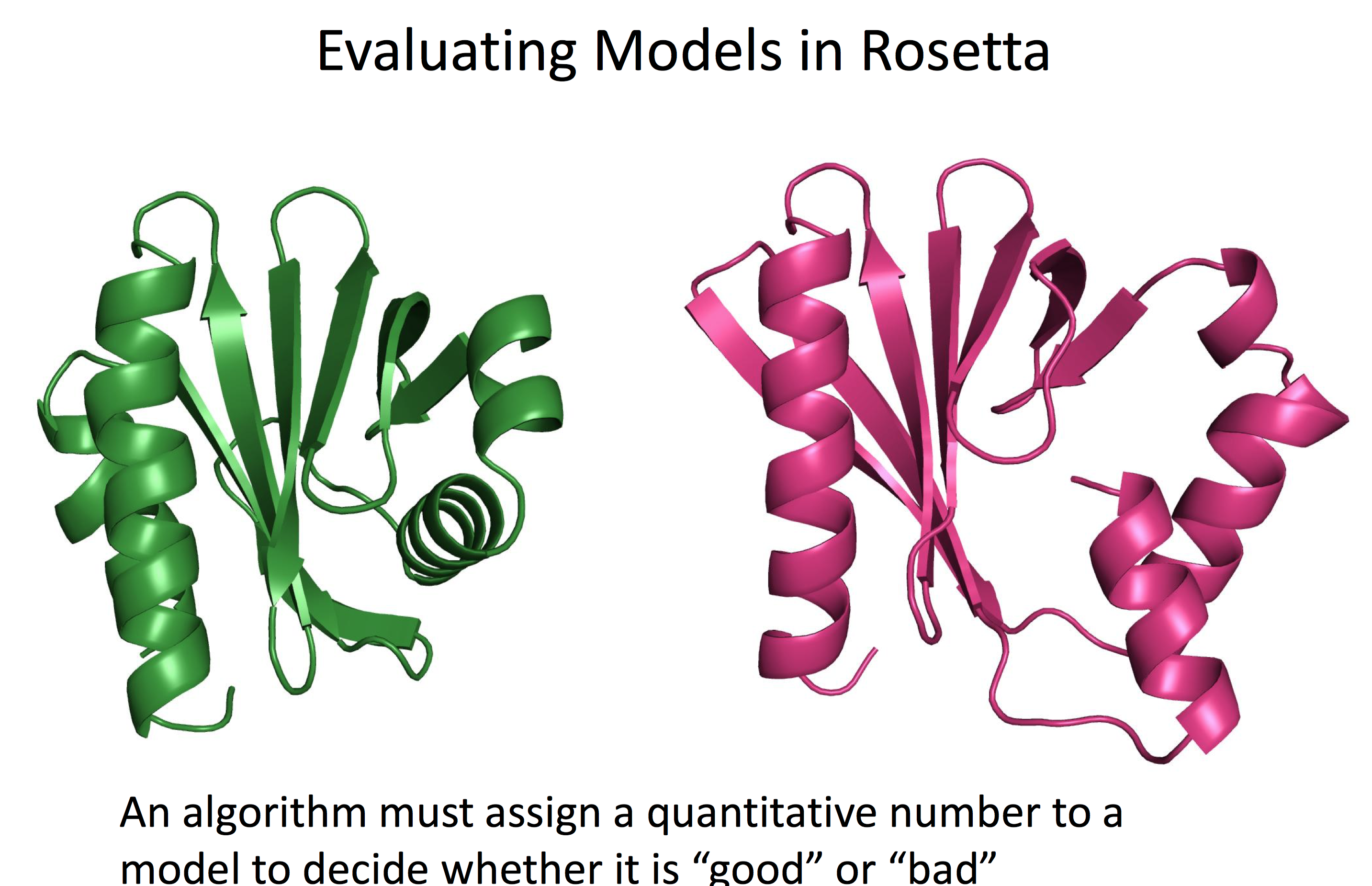
读者可自行凭借直觉评估,上图中绿色和粉红色的两个蛋白质预测的结构哪个更接近于真实的情况?哪个模型更加地可靠呢?
如果是比较有经验的人士,会认为绿色的模型更接近于真实的蛋白结构,原因是蛋白质往往依靠疏水相互作用驱使折叠成能量最低的状态,而粉红色的右下角处的α螺旋与周围的结合紧密程度较差,蛋白质存在空腔。如果我们使用Rosetta能量函数去打分,那么绿色模型的能量也显著低于粉红色的模型。也就是说Rosetta的能量函数与我们直觉的判断结果一致。那么有趣的问题来了,Rosetta能量函数为何可以较为准确地评估模型的好坏?
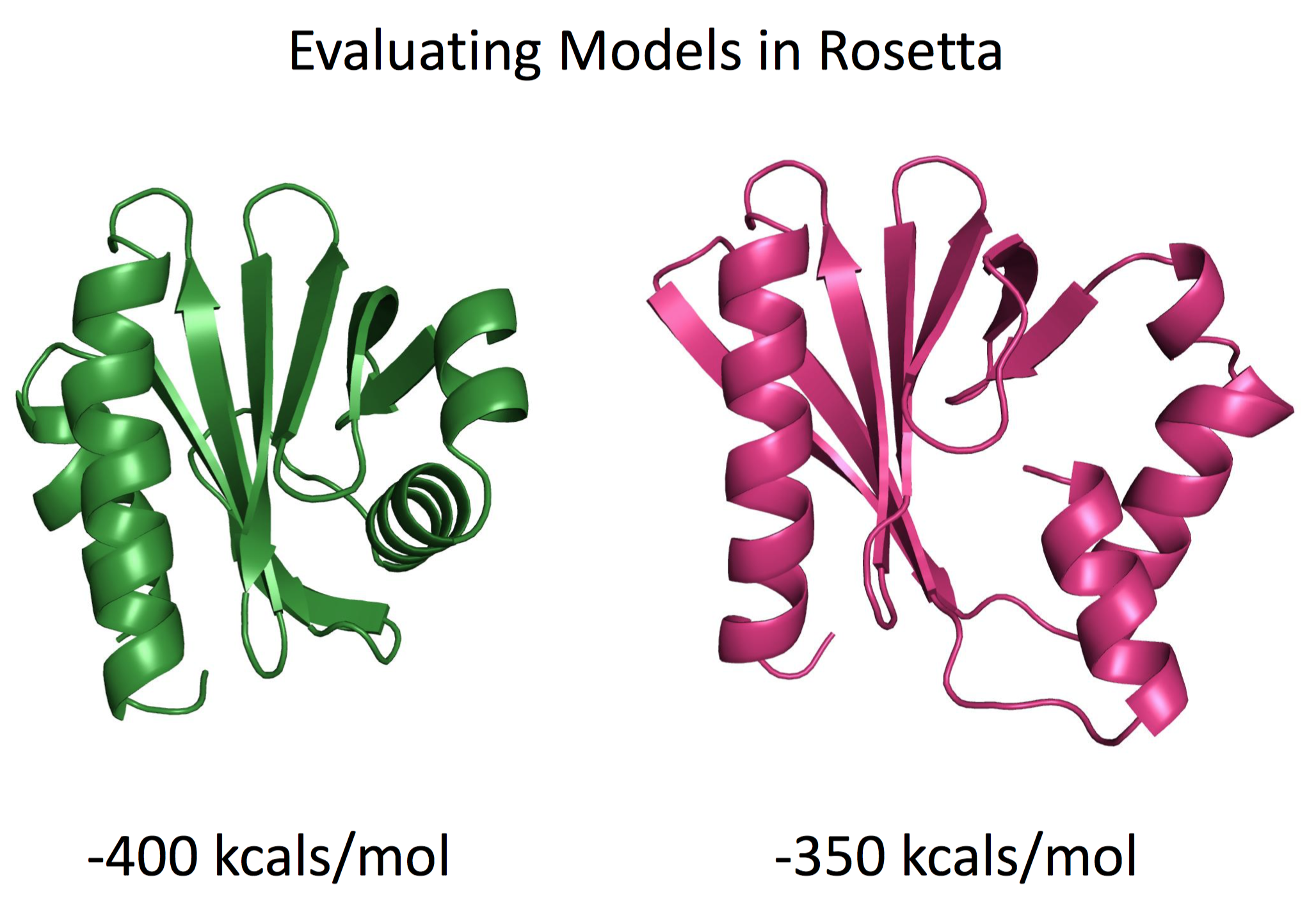
二、Rosetta能量项类型与分类
Rosetta能量函数由一系列可衡量的几何统计或经典物理相互作用能量经过加权后得到的函数形式。在给定原子坐标的条件下,评估原子之间的相互作用能量的大小。在之前版本的Rosetta中,能量的单位是REU(Rosetta Energy Unit),而最新版本的full-atom打分函数(ref2015))经过矫正,目前单位为kcals/mol。
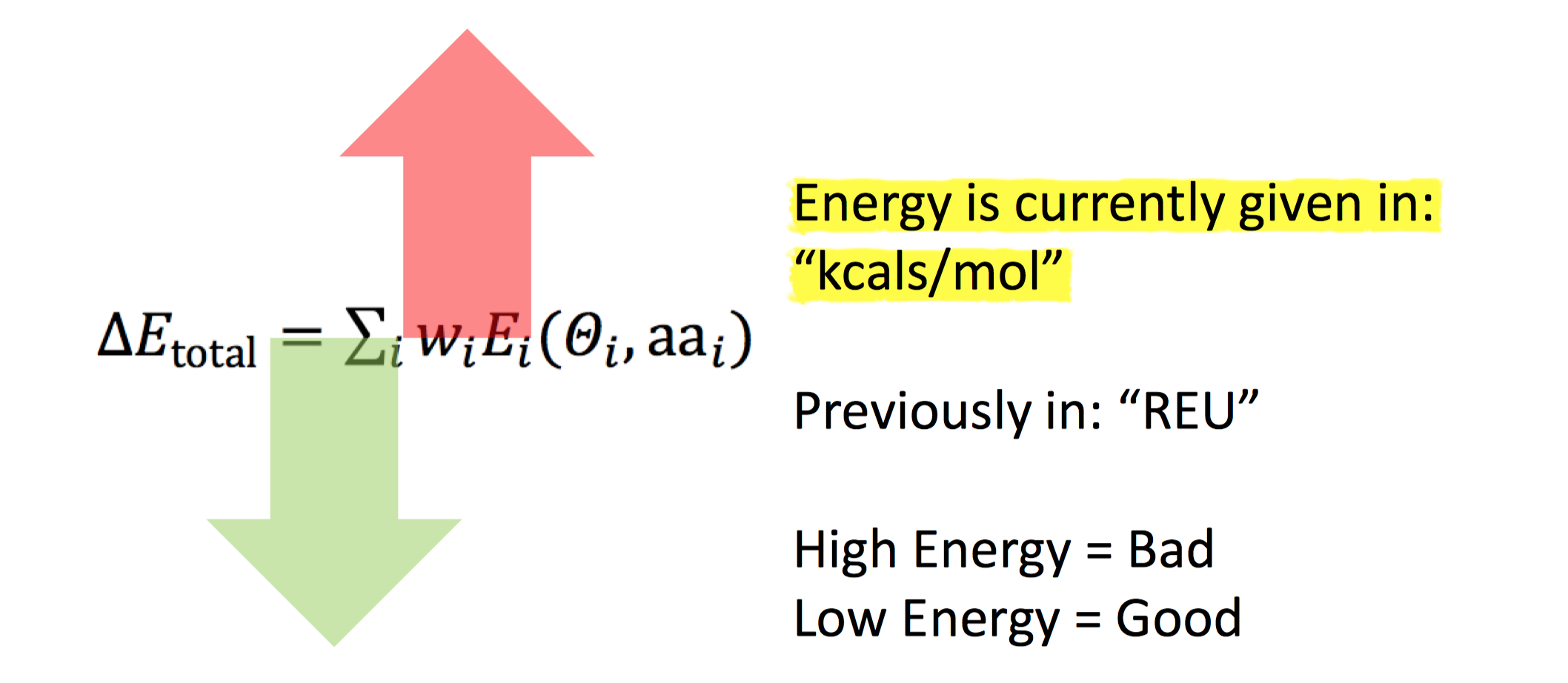
从相互作用类型来分,Rosetta的打分项通常分为3类:
One Body:通常这类打分项只和单个氨基酸构象有关,比如骨架的二面角,侧链的rotamer构象等
Two Body:这类打分项与两个氨基酸有关,比如范德华力相互作用,静电相互作用
Whole Body:从整体几何性质或其他的指标考虑蛋白质的能量,如蛋白质的回旋半径,二级结构组成等可统计的量

从打分项的拟合方法上来区分,可分为物理势能项和统计势能项:
- 物理势能项通常是从物理上定义的分子相互作用经典公式去计算得到的值,比如范德华力的LJ势函数,库仑力的静电势函数。
- 统计势能项,一般是从蛋白质结构数据库中统计得到。这里有个比较重要的前提假设就是,在数据集中,出现概率越高的性质或则构象,其能量越低,出现罕见的则能量越高(玻尔兹曼分布),因此可以通过测定频率直接取对数近似能量的大小值。比如,我通过统计蛋白质主链上的phi, psi角的分布情况就可以统计得到Ramachandran图,其中点越富集说明这些主链构象的能量越低,在自然界中频繁被观测到。

简单来说在得到了多个打分项后,通常会在给定一些数据集条件下,通过拟合权重,就可以表现比较良好的打分函数,Rosetta能量函数拟合也是如此。举个例子,通过ab-inito的fragment组装得到了大量预测的蛋白质结构模型,通过尝试调整和组合每一项的打分权重,试图将与晶体最接近的那个模型能量拟合为最低的能量状态。

三、Rosetta能量项具体的解释
该章节设计的计算公式较多,如果觉得比较难理解,就了解下大致有哪些项组成,分别是代表什么含义即可。
在Rosetta中,氨基酸的模型有两种,一种是粗粒化模型,一种是全原子模型。
在Centroid模型下,氨基酸的侧链被一个有一定半径大小的粗粒化球所替代,而在full-atom模型下,所有的侧链原子被显式的表示出来。因此Rosetta的打分函数的项的组成也会根据选用的氨基酸模型不同而不同。

在粗粒化模型下,Rosetta打分项组成可见连接: Centroid score terms
centroid打分函数的详细来历的解读可参考: https://zhuanlan.zhihu.com/p/73035074
本文仅阐述与与Full-atom打分函数 (ref2015)相关的项, 在全原子模型下,Rosetta打分项组成可见连接:Full-atom score terms

1. LJ势
描述范德华力相互作用的函数,与两个原子间的距离有关,参数来源于CHARMM力场,fa_atr/fa_rep共同描述两个原子间,短距离的范德华力。在Rosetta中范德华力被拆分成两个独立的项,并做了smooth处理。fa_atr为Lennard-Jones LJ6-12势中的吸引项,fa_rep为排斥项。将范德华力拆分后,Roseta可以更加方便地进行模拟退火,如单独设置个调整fa_rep和fa_atr的权重。fa_intra_rep与fa_rep类似,引入该项是因为fa_dun常常低估了氨基酸残基内部的原子的冲突。

E_{\mathrm{atr}}=\sum_{i, j} w_{i, j}^{\operatorname{conn}}\left\{\begin{array}{cc}{-\varepsilon_{i, j}} & {d_{i, j} \leq \sigma_{i j}} \\ {\varepsilon_{i, j}\left[\left(\frac{\sigma_{i j}}{d_{i j}}\right)^{12}-2\left(\frac{\sigma_{i j}}{d_{i j}}\right)^{6}\right]} & {\sigma_{i, j}<d_{i, j} \leq 4.5 \mathrm{A}} \\ {f_{\mathrm{poly}}\left(d_{i, j}\right)} & {4.5 \mathrm{A} \leq d_{i, j} \leq 6.0 \mathrm{A}} \\ {0} & {6.0 \mathrm{A} \leq d_{i, j}}\end{array}\right.
E_{\mathrm{rep}}=\sum_{i, j} w_{i, j}^{\operatorname{conn}}\left\{\begin{array}{cc}m_{i, j} d_{i, j}+b_{i, j} \qquad \quad d_{i, j} \leq 0.6 \sigma_{i, j}\\\varepsilon_{i, j}\left[\left(\frac{\sigma_{i, j}}{d_{i, j}}\right)^{12}-2\left(\frac{\sigma_{i, j}}{d_{i, j}}\right)^{6}+1\right] \quad 0.6 \sigma_{i, j}<d_{i, j} \leq \sigma_{i, j}\\0 \qquad \sigma_{i, j}<d_{i, j}\end{array}\right.
在计算atr和rep时都引入共价连接权重(connectivity weight)来确保一级序列上相隔多少个键以内范德华力的权重变化,避免导致相邻的氨基酸之间存在异常大的排斥力。
w_{i, j}^{\mathrm{conn}}=\left\{\begin{array}{cc}{0} & {n_{i, j}^{\mathrm{bonds}} \leq 3} \\ {0.2} & {n_{i, j}^{\mathrm{bonds}}=4} \\ {1} & {n_{i, j}^{\mathrm{bonds}} \geq 5}\end{array}\right.
2. 静电势
该项距离依赖型的静电势函数,从CHARMM中衍生优化而来,该项的值与两个原子的电荷数、环境的介电常数、原子的距离有关。在Rosetta中的一个重要假设是库仑势中的介电常数是与两个电荷原子之间的距离决定的,如果两个原子的距离比较近,那么假设他们之间可能只有真空或则一些极性相互作用的原子,因此介电常数比较小,如果距离非常地远,那么他们之间可能填充了水或非极性的物质(如蛋白质的内核),那么介电常数假设为比较大。介电常数的值根据二者的距离发生变化,是通过一个sigmoidal function进行拟合而得ε_core=6, ε_solvent=80。

\epsilon\left(d_{i, j}\right)=g\left(\frac{d_{i j}}{4}\right) \epsilon_{\mathrm{core}}+\left(1-g\left(\frac{d_{i j}}{4}\right)\right) \epsilon_{\mathrm{solvent}}
g(x)=\left(1+x+\frac{x^{2}}{2}\right) \exp (-x)
静电势项做了截断处理,只有5.5埃范围内的静电势才会被计算。当距离小于1.4埃时,静电势曲线斜率为0。在1.45-4.5埃范围内使用三次函数拟合,进行曲线平滑处理,避免由于截断处理带来的不连续性。
E_{\mathrm{fa} \text { elec }}=\sum_{i, j} w_{i, j}^{\mathrm{conn}}\left\{\begin{array}{cc}E_{\mathrm{elec}}\left(i, j, d_{\min }\right) \qquad d_{i, j}<1.45 \hat{\mathrm{A}}\\f_{\text { poly }}^{\text { eleclow }}\left(d_{i, j}\right) \quad 1.45 \hat{A} \leq d_{i, j}<1.85 \mathrm{A}\\E_{\mathrm{elec}}\left(i, j, d_{i, j}\right) \quad 1.85 \hat{A} \leq d_{i, j}<4.5 \hat{A}\\f_{\text { poly }}^{\text { elec,hi }}\left(d_{i, j}\right) \qquad 4.5 A \leq d_{i, j}<5.5 \hat{A}\\0 \qquad 5.5 \hat{A} \leq d_{i, j}\end{array}\right.
3 氢键相互作用
Rosetta使用hbond项与fa_elec一同计算氢键的能量。
hbond项是根据Top8000高精度结构数据库中衍生得到的,首先通过将蛋白质内部的极性相互作用对的分离,并拟合了它们的二面角、键角、供体受体原子的距离等参数的能量分布。
目前hbond项与4个自由度有关: BAH、 B2BAH、 HA、 AHD (简单来说就是统计氢键相关原子的键角、二面角、距离等),根据原子轨道的杂化情况不同, BAH与 B2BAH拟合成两种类型的能量密度分布,受体原子杂化类型由 设置。
E_{\mathrm{hbond}}=\sum_{H, A} w_{H} w_{A} f\left(E_{\mathrm{hbond}}^{H A}\left(d_{H A}\right)+E_{\mathrm{hbond}}^{A H D}\left(\theta_{A H D}\right)+E_{\mathrm{hbond}}^{B A H}\left(\theta_{B A H}\right)+E_{\mathrm{hbond}}^{B_{2} B A H}\left(\rho, \phi_{B_{2} B A H}, \theta_{B A H}\right)\right)
氢键项的能量同时与供体和受体的原子类型有关,不同原子权重有对应的设置。

最后通过函数f(x)进行平滑处理, 避免非连续性:
f(x)=\left\{\begin{array}{cc}{x} & {x<-0.1} \\ {-0.025+\frac{x}{2}+2.5 x^{2}} & {-0.1 \leq x<0.1} \\ {0} & {0.1 \leq x}\end{array}\right.
具体的hbond项类型可分为:
- hbond_sr_bb: 短距离骨架氢键,如α螺旋的骨架氢键项
- hbond_lr_bb: 远距离的骨架氢键,如β折叠或loop中的骨架氢键项
- hbond_sc_bb: 侧链与骨架之间的氢键项
- hbond_sc: 侧链与侧链之间的氢键项
为了避免重复计算,如果骨架与骨架之间已经产生了氢键,那么侧链与骨架原子之间的氢键计算被排除。
注意: 因为Rosetta中氢键相互作用的计算为Two Body的形式,因此无法很好地描述氢键网络等三体以上的相互作用
4. 二硫键键能 (dslf_fa13)
Rosetta二硫键项也是与hbond类似,从数据库衍生得来,与具体二硫键的构象有关。二硫键有6个自由度: S-S硫原子间的距离、两个Cβ-S-S的键角、Cβ-S-S-Cβ二面角以及两个Cα-Cβ-S-S二面角。当实际二硫键的数据偏离这些平均角度时,键能越大。
E_{\mathrm{dslf}_{-} \mathrm{fa} 13}= \sum_{S_{1}, S_{2}} E_{\mathrm{dslf}}^{S S}\left(d_{S S}\right)+E_{\text { dslf }}^{C S S}\left(\theta_{C_{\beta 1} S S}\right) +E_{\mathrm{dslf}}^{C S S}\left(\theta_{C_{\beta 2} S S}\right) + \\ E_{\text { dslf }}^{C_{\alpha} c_{\beta} S S}\left(\phi_{C_{\alpha 1}} c_{\beta 1} s s\right) + E_{\mathrm{dslf}}^{C_{\alpha} c_{\beta} S S}\left(\phi_{C_{\alpha 2} C_{\beta 2} S S}\right)+ E_{\mathrm{dslf}}^{C_{\beta} S S C_{\beta}}\left(\phi_{C_{\beta 1} S S C_{\beta 2} )}\right.

5. 溶剂化能相关项 (fa_sol/lk_ball_wtd/fa_intra_sol)
天然的蛋白质折叠倾向于形成疏水内核,使得在外部的疏水残基数量尽可能的少(疏水力)。但是显式地将分布在蛋白质表面的水分进行建模过于耗时,因此在Rosetta中,采用的是Lazaridis-Karplus (LK) implicit Gaussian exclusion模型计算(有兴趣可以去了解下),该模型通过计算两个原子间的距离来近似计算原子间排除水分子所需要消耗的能量。
在Rosetta中溶解模型由两项组成:
- fa_sol: 各向同性的溶解自由能, 假设一个原子周围的水分子是均匀分布状态,用于评估非极性原子
- lk_ball_wtd: 各向异性的溶解自由能, 假设水分子非均匀分布,用于评估能极性原子。

在Rosetta中,各向同性的溶解自由能的变化采取了分段函数的形式,避免在fa_rep项较弱的时候,fa_solv项过度促进原子间距离拉近,做了分段的平滑处理。因此溶解自由能与两个原子间的距离相关。
f_{\text {desolv }}=-V_{j} \frac{\Delta G_{i}^{\text {free }}}{2 \pi^{\frac{3}{2}} \lambda_{i} \sigma_{i}^{2}} \exp \left(-\left(\frac{d-\sigma_{i, j}}{\lambda_{i}}\right)^{2}\right)

E_{\mathrm{fa}{\_\mathrm{sol}}}=\sum_{i, j} w_{i, j}^{\mathrm{conn}}\left(g_{\mathrm{desolv}}(i, j)+g_{\mathrm{desolv}}(j, i)\right)
在最新的能量函数版本中,引入了LK势,区分了非极性和极性原子的溶剂化能的计算。该各向异性模型增加了在水可能形成氢键相互作用的位点附近阻塞极性原子的去溶剂化能的惩罚。做出了更加准确的评估。
6 主链二面角统计项 (rama_prepro/p_aa_pp)
与骨架二面角分布统计相关的项。

rama_prepro
直接从数据库中得到的统计量,其含义为给定一种氨基酸类型时,其骨架二面角的概率分布,分为i+1为脯氨酸和非脯氨酸两种情况。
如果模型中二面角落于频率分布高的格点区域,则能量越低,骨架构象合理的可能性越高。当偏离这些高频率分布的区域时,骨架二面角的能量越高。
E_{\text { rama pre-pro }}=\Sigma_{i}\left\{\begin{array}{cc}{-\ln \left[P_{\text { reg }}\left(\phi_{i}, \psi_{i} | \text { aa }_{i}\right)\right]} \\ {-\ln \left[P_{\text { prepro }}\left(\phi_{i}, \psi_{i} | \text { aa }_{i}\right)\right]}\end{array}\right.
- P(reg)为C端或i+1为非脯氨酸的概率
- P(prepro)为i+1为脯氨酸时的概率
p_aa_pp
通过贝叶斯定理进行的转化统计所得项,含义是在目前的phi/psi区间内,出现某一种氨基酸的概率。用于评估氨基酸的可替换性,与突变设计相关的能量项,也可以理解为设计得到的氨基酸与骨架匹配程度的一个评估。
P(\text { aa } | \phi, \psi)=\frac{P(\phi, \psi | \text { aa }) P(\text { aa })}{\sum_{\text { aal }} P(\phi, \psi | \text { aa' }) P(\text { aal })}
E_{p_{-} a a_{-} p p}=\sum_{r}-\ln \left[\frac{P\left(a a_{r} | \phi_{r}, \psi_{r}\right)}{P\left(a a_{r}\right)}\right]
7 侧链构象能量
此项用于评估侧链构象的能量值大小,计算原理是从dunbrack rotamer数据库中查询该Rotamer类型出现的概率大小,并且与rotamer的平均构象的偏差值来评估能量大小。如果选择的Rotamer在phi/psi范围内出现的概率高,且构象与平均构象越接近时,Rotamer的内在能量越低。
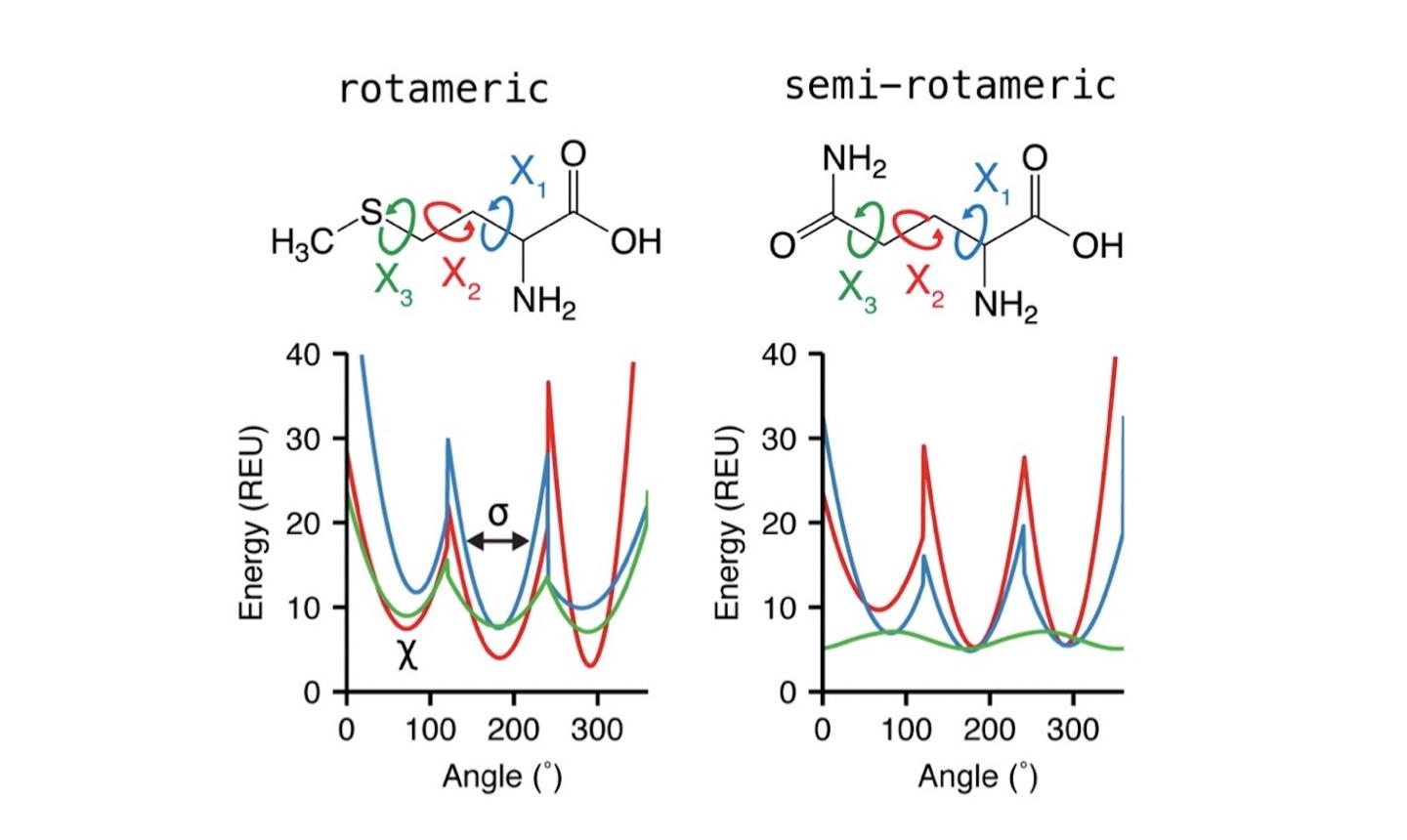
rotamer与non-rotameric分类:
Dunbrack rotamer库将氨基酸侧链的chi二面角分为两类: rotameric和non-rotameric。
rotameric为sp3杂化的chi二面角(chiK),因此有很强的立体位阻效应, 其具体值偏向于分布在60°(g+)、180°(t)以及-60°(g-)这三个区间附近。
non-rotameric主要指末端的chi二面角(chiT),主要为sp2杂化类型,存在于8种氨基酸中(Asp, Asn, Gln, Glu, His, Phe, Tyr, Trp)。这类末端chi二面角的分布与其前面的chi角分布区间、phi/psi角有关。

Dunbrack rotamer库中的数据记录了每一种rotamer的类型,出现的概率以及每个chi角的平均值和方差值。可用于后续的计算。

因此以下三项概率,推算某个Rotamer的出现概率:
- P(rot | φ, ψ, aa): 某个氨基酸的Rotamer类型(如: (g+,g-))在当前phi/psi格点中出现的概率
- P(χk | φ, ψ, aa, rot): 在某个氨基酸的Rotamer类型, phi/psi格点中,rotameric的具体chi角出现的频率
- P(χT| φ, ψ, aa, rot): 某个氨基酸的Rotamer类型,phi/psi格点中,non-rotameric的具体chi角的出现的频率
因此计算特定构象rotamer的出现的概率P(χ | φ, ψ, aa) 可以根据以下公式计算,当氨基酸为non-rotameric类型时,P(χT | φ, ψ, aa, rot)恒等于1。
简单理解(条件概率): 在rotamer类型出现概率的前提下,具体rotamer出现的概率。 如果只考虑1个χ角的情况,如丝氨酸。通过条件概率公式可知: p(χ1)=p(rot)p(χi1|rot),如果考虑2个χ角的氨基酸(rotameric),那么p(χ1,χ2)=p(rot)p(χ1|rot)p(χ2|rot),此处χ1,χ2相互独立。
P(\chi \mid \phi, \psi, \text { aa })=P(\operatorname{rot} \mid \phi, \psi, \text { aa })\left(\prod_{k<T} P\left(\chi_{k} \mid \phi, \psi, \text { rot,aa }\right)\right) P\left(\chi_{T} \mid \phi, \psi, \text { rot,aa }\right)
此处为了计算p(χ1|rot),也就是公式中P(χk | φ, ψ, aa),假定了chi角在rotamer类型附近的分布类似高斯分布。由此似然出了一个概率p(χ1|rot),因此公式中P(χk | φ, ψ, aa)的概率与该phi, psi格点中该rotamer类型的平均χk角偏差度有关,当值偏离平均值时,概率就越低。
(为什么要求这一项?因为Dunbrack rotamer lib中拟合的是一个rotamer类型分布的区间概率,而不是一个具体的χ角出现概率,因此这里使用了rotamer的χ角平均值和方差值来拟合了一个概率)
P\left(\chi_{k} \mid \phi_{k}, \psi_{k}, \mathrm{rot}\right)=\exp \left(-\frac{1}{2}\left(\frac{\chi_{k}-\mu_{\chi_{k}}(\phi, \psi \mid \mathrm{rot}, \text { aa })}{\sigma_{\chi_{k}}(\phi, \psi \mid \mathrm{rot}, \text { aa })}\right)^{2}\right)
对概率取-ln对数可得能量rotamer的能量值:
E_{{fa}_{-}{dun}}=\sum_{r}-\ln \left(P\left({rot}_{r} | \phi_{r}, \psi_{r}, {aa}_{r}\right)\right)+ \sum_{k<T_{r}} \frac{1}{2}\left(\frac{\chi_{k, r}-\mu_{\chi_{k}}\left(\phi_{r}, \psi_{r} | {rot}_{r}, {aa}_{r}\right)}{\sigma_{\chi_{k}}\left(\phi_{r}, \psi_{r} | {rot}_{r}, {aa}_{r}\right)}\right)^{2} -\ln \left(P\left(\chi_{T_{r}, r} | \phi_{r}, \psi_{r}, {rot}_{r}, { aa }_{r}\right)\right)
8 特殊氨基酸相关项
对脯氨酸、酪氨酸还有附加的项来控制正确的侧链构象,而omega项用于控制稳定的肽键平面。

omega项
肽键二面角会根据phi/psi角度变化,但基本固定在180°(trans-)或0°(cis-),当肽键二面角偏离时,生成惩罚。
E_{\mathrm{omega}}=\sum_{r} \ln \left(\frac{1}{6 \sqrt{2 \pi}}\right)-\ln \left(\frac{1}{\sigma_{\omega}\left(\phi_{r}, \psi_{r} | \operatorname{aa}_{r}\right) \sqrt{2 \pi}}\right)+\frac{\left(\omega_{r}-\mu_{\omega}\left(\phi_{r}, \psi_{r} | \operatorname{aa}_{r}\right)\right)^{2}}{2 \sigma_{\omega}^{2}\left(\phi_{r}, \psi_{r} | \text { aa }_{r}\right)}
pro_close项
脯氨酸的肽键二面角项,用于惩罚开环的脯氨酸构象。通过统计脯氨酸ω'二面角分布以及chi3角的分布来实现。
E_{\mathrm{pro}_{-} \mathrm{close}}=\sum_{r \in \mathrm{Pro}}\left\{\begin{array}{c}\frac{\left(\omega_{r}^{\prime}-\mu_{\omega^{\prime}}\right)^{2}}{\sigma_{\omega^{\prime}}^{2}}+\frac{\left\|\mathbf{N}_{r}-\mathbf{N}_{v, r}\right\|^{2}}{\sigma_{\mathrm{N}, \mathrm{N}_{\mathcal{V}}}^{2}}\\\frac{\left\|\mathbf{N}_{r}-\mathbf{N}_{v, r}\right\|^{2}}{\sigma_{\mathrm{N}, N_{\nu}}^{2}}\end{array}\right.
- 第一项为r非N端氨基酸
- 第二项为r为N端氨基酸
yhh_planarity项
与脯氨酸类似,酪氨酸的chi3角也需要特殊处理,因为羟基的氢通常与苯环在同一个平面内,因此当氢原子偏离时就会生成惩罚的能量。
E_{\text { yhh-planarity }}=\sum_{i} \frac{1}{2}\left[\cos \left(\pi-2 \chi_{3, i}\right)+1\right]
9 解折叠自由能项 (Ref)
上述的所有能量项都是在蛋白质折叠态下统计的值,而我们在进行但计算序列设计时,不同氨基酸类型的转换过程中需要计算 G_Mutation,这一项的计算需要涉及到解折叠态下的焓变与熵变的计算。这部分是无法直观统计的。因此在Rosetta中进行了取巧来近似这项能量。


首先假设在固定骨架结构的前提下,该结构的天然氨基酸序列是能量最低的状态,通过调整ref项的权重,让基于骨架设计出来的序列与天然序列的相似度尽可能地高。
参考
- Alford RF, et. al, The Rosetta All-Atom Energy Function for Macromolecular Modeling and Design. Journal of Chemical Theory and Computation, 2017. 13 (6), 3031-3048
- Park H, et. al Simultaneous Optimization of Biomolecular Energy Functions on Features from Small Molecules and Macromolecules Journal of Chemical Theory and Computation, 2016. 12 (12), 6201-6212

