抽样分布篇之七：抽样分布总结

三大抽样分布和正态分布共同构成了现代数理统计学的基础，也在各行各业有了各自的应用。比如六西格玛涉及的质量管理领域，就发展出了统计过程控制、过程能力、测量系统分析等等应用，而在医学领域，属性数据(分类数据)的分析方法有非常广泛的应用。

在看了前面几篇文章后，可能还是有不少人对其概念和应用不太清楚，这里加以总结。

抽样分布可以分为两类：一类是关于均值的分布：正态分布和t-分布；另一类是关于方差的分布：\chi ^{2} -分布和F-分布。

首先要明确的是，所有分布的前提是所收集的样本要服从正态分布，这需要首先进行正态分布的拟合检验，即使是大样本的情况下，样本正态的情况下分析结论也要更准确一些。

均值的分布

这要分两种情况：总体方差\sigma ^{2} 是否已知。

如果总体方差已知，则样本均值可以构建下面的统计量

这个统计量服从标准正态分布N(0,1)。

如果总体方差未知，则可以用样本方差代替总体方差，构建下面的统计量

这个统计量服从t-分布t(n-1)，n-1为自由度。t-分布的形状与自由度有关，自由度越小，则分布曲线越“胖”，自由度越大，分布曲线约接近正态分布。一般在自由度超过30时，基本上就和正态分布差不多了，也可以用正态分布来分析。

方差的分布

\chi ^{2} -分布是针对单个正态总体的样本方差分布，依据总体均值μ是否已知分为两种情况。

如果总体均值μ已知，则样本方差可以构建以下的统计量

这个统计量服从\chi ^{2} \left( n \right) 分布，自由度为n。

如果总体均值μ未知，则用样本均值\bar{X} 来代替，这样上述统计量就改为

这个统计量服从\chi ^{2} \left( n-1 \right) 分布，自由度为n-1。两个统计量自由度差1个，是因为在总体均值未知时需要用样本均值来估计，用掉了1个自由度。

F-分布是针对两个正态总体的样本方差之比的分布。

假设两个独立的正态总体方差相等，在这两个总体中分别抽取1个样本，样本量分布为m、n，用两个样本方差构建以下的统计量

这个统计量服从分子自由度为m-1，分母自由度为n-1的F(m-1,n-1)分布。

F-分布应用非常广泛，尤其是在判断两总体方差是否相等以及方差分析中，在回归分析和DOE中也有重要的应用。

根据这几个分布的性质，还可以导出其它的统计量，比如两个均值之差的分布等，感兴趣的请参考相关的书籍，这里不再赘述。

对于服从二项分布的总体比例来说，样本的比例同样服从二项分布。当np和n(1-p)均大于5时，可以用正态来近似，其均值和方差分别为

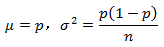
这些统计量及其分布非常重要，是很多统计分析方法的基础。通过计算样本的相关统计量，可以依据这些统计量的分布做出恰当的判断。在比较分析中，大家会看到上面列出的这些统计量的大量应用。

请关注我的微信公众号：张老师漫谈六西格玛