色彩空间表示与转换
前一篇文章 讲述了色彩空间的基础,我们看到人类的色视觉可以用一个三维的线性空间表示,人类对色彩的感知,相当于是在光谱分布这样一个无穷维的函数空间(巴拿赫空间)中,进行了一个三维投影。在此基础上,简单介绍了两个重要的线性色彩空间, CIE 1931 RGB 和 CIE 1931 XYZ,这两个色彩空间包含了所有人类可以感知的色彩。通过色匹配函数(Color Matching Function, CMF),可以将任何一种物理上的光谱分布,转换到线性色彩空间中。
虽然是同样一个线性空间,由于选取的基底不同,表示的形式也会不同,表达能力和方便程度也会有所不同。为了不同的用途和目的,人们发展了很多不同的线性色彩空间的表达形式。此外,人类的色视觉在某些方面还存在一定程度的非线性,所以在线性色彩空间基础上人们又发展了一些非线性的色彩空间。
由于 CIE RGB 和 CIE XYZ 两者其实是同一个线性空间的不同表达,因此两者的转换可以通过转换矩阵实现。限于篇幅,上一篇文章 中对这个转换矩阵是怎么来的一笔带过了,在这篇文章中将会详细描述中间的计算过程。
1 CIE RGB 和 CIE XYZ
在前一篇文章中我们已经了解到,以色匹配函数作为基底,将物理上的光谱分布投影到三维空间中,就可以得到 CIE RGB 和 CIE XYZ 色彩空间。 CIE RGB 的色匹配函数(归一化后)是这样的:

注意这里进行了归一化处理,因此曲线与上一篇文章中的曲线形状有变化。为了消除部分负数坐标,我们变换到 CIE XYZ 空间,满足一些约束条件:
- 所有坐标都是正的保持等能点(equal energy point)作为白色
- 使得新的 Y 坐标能够代表明度,也就是使得新的 Y 坐标等于视觉的明度响应
- 使得新的 Z 坐标在红光端保持为 0
- 使得所有色彩尽可能充满新的空间
在这些约束条件下,CIE 委员会设计了这两个空间之间最初的转换矩阵:
\left[\begin{array}{c} X \\ Y \\ Z \end{array}\right] = \left[\begin{array}{ccc} 2.7688 & 1.7517 & 1.1301 \\ 1.0000 & 4.5906 & 0.0601 \\ 0 & 0.0565 & 5.5942 \end{array}\right] \left[\begin{array}{c} R \\ G \\ B \end{array}\right]以及反变换的矩阵
虽然最开始是从 CIE RGB 转换到 CIE XYZ 空间的,但之后由于历史原因和技术原因,使得 CIE XYZ 空间更为广泛接受,逐渐作为更常用的转换空间。在最新的官方资料中,只保留了 XYZ 空间的色匹配函数,已经没有 RGB 空间的色匹配函数了。
2 色品图(Chromaticity Diagram)
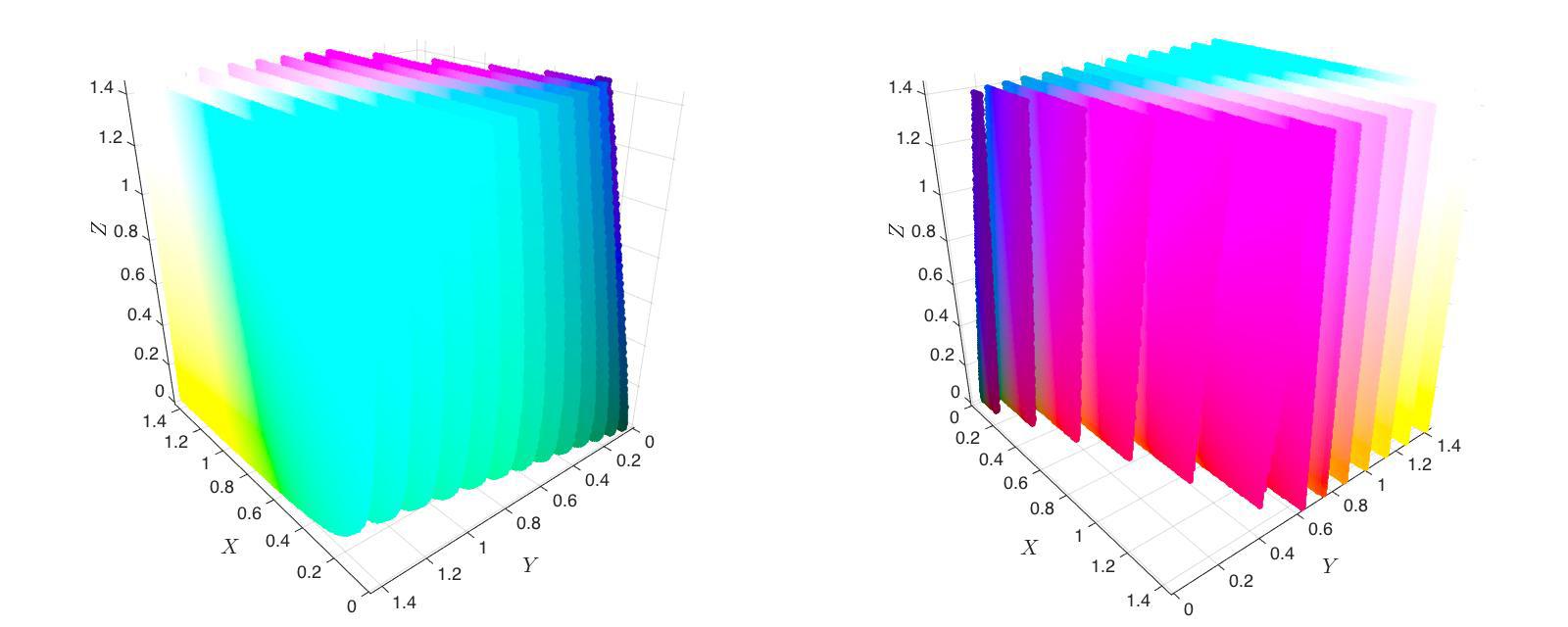
那么,各个颜色在 CIE XYZ 空间中是怎么分布的呢?由于实际中不可能有光线的减法,所有的运算都是「锥组合」,因此可以想见实际所有可能的颜色,在 XYZ 空间中应该位于一个以原点为顶点的 「锥体」中(比如 xyz 三个正半轴围起来的第一卦限就是一个锥体)。我们把 CIE XYZ 空间切片看看(左右两列是从两个不同的视角进行观察):



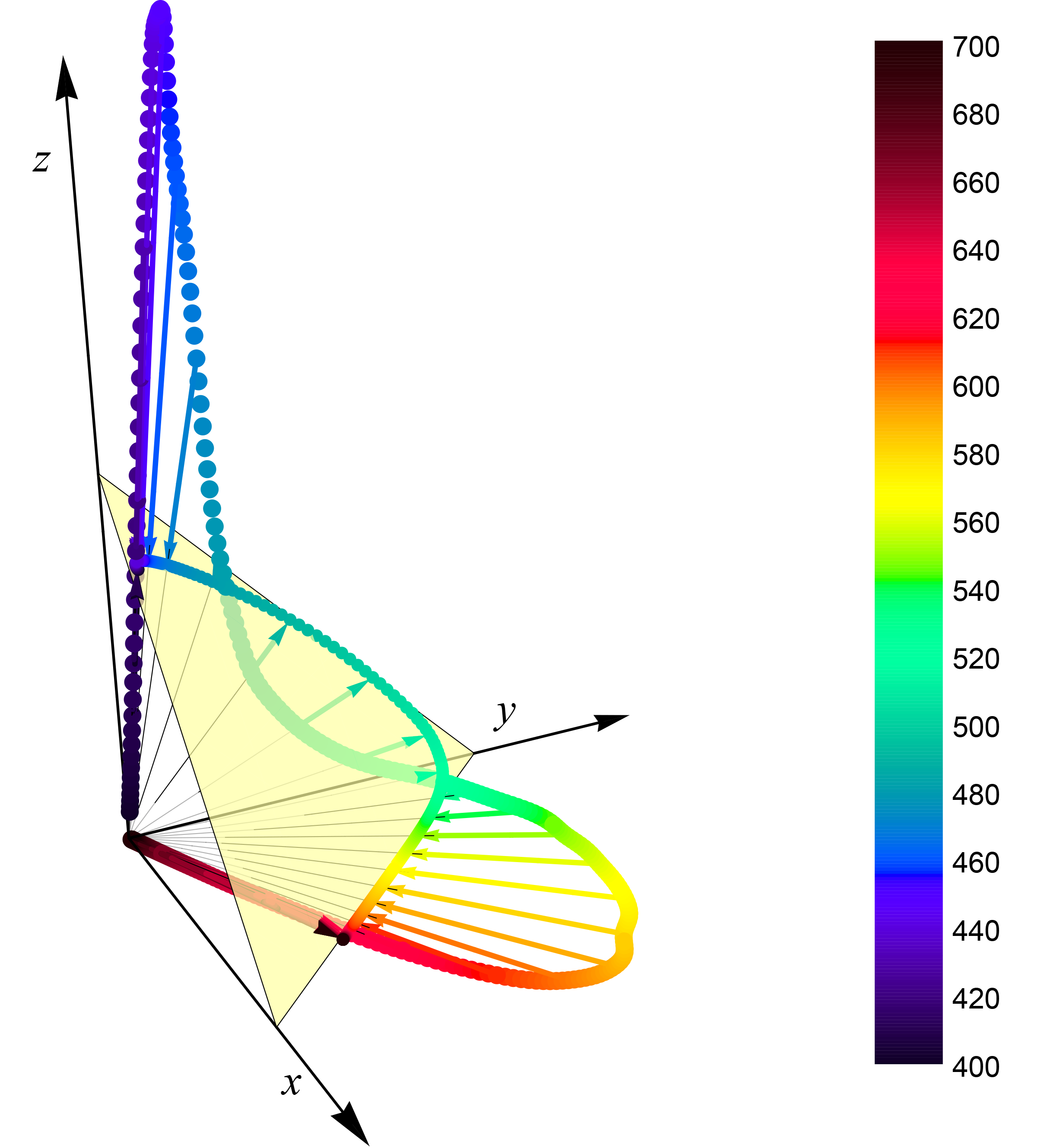
可以感受到约靠近原点的切片越小,这正是锥体的表现。然而这个锥体到底是什么形状呢?如果把纯光谱色画在 CIE XYZ 空间中,得到下图这样的曲线。连接原点与这条曲线得到的无数条射线,包围出来一个「锥体」,这个锥体就是人所能感知的所有色彩。注意与上图(尤其是右侧一列,与下图视角接近)比较,可以清楚地看到红色一侧和蓝紫色一侧围出的倾斜的边界。

图中蓝色数字标明了纯光谱色对应的波长。
3 与其他 RGB 空间的转换
之前的文章说到,定义一个 RGB 空间,关键在于两个参数:1. RGB 三点的坐标;2. 白色点的位置。这里就以 sRGB 空间为例,说说如何根据这两个参数确定转换关系的。
根据定义,sRGB 的三原色以及白色点的 XYZ 坐标是:

白色点的意义在于校准三原色在向量空降中的长度,使得当 RGB = (1, 1, 1) 的时候正好对应的是白色。也就是列出这个方程:
W = w_r R + w_g G + w_b B或者写成矩阵形式
W = [R, G, B]\boldsymbol{w}求解出 w_r, w_g, w_b 各个系数。这是个三元一次方程,在计算机上非常容易求解,即使手工求解也不难。
\boldsymbol{w} = [R, G, B]^{-1}W对于 sRGB 的情况来说,带入数字,可得
\boldsymbol{w} = [R, G, B]^{-1}W = \left[\begin{array}{ccc} 0.64 & 0.30 & 0.15 \\ 0.33 & 0.60 & 0.06 \\ 0.03 & 0.10 & 0.79 \end{array}\right]^{-1} \left[\begin{array}{c} 0.95047 \\ 1.00000 \\ 1.08883 \end{array}\right] = \left[\begin{array}{c} 0.6445 \\ 1.1919 \\ 1.2029 \end{array}\right]接下来,对于某一种颜色 C = (x, y, z),它对应的 sRGB 坐标是多少呢?也就是如果将校正长度后的 RGB 三原色作为新的基底,那么各个分量都是多少呢?我们可以写出新的方程:
或者写成矩阵形式
所以,从 sRGB 到 XYZ 的转换矩阵就是:
那么从 XYZ 转到 sRGB 的矩阵就是他的逆矩阵:
注意到,这里的矩阵中出现了负数,也就是说,从 CIE XYZ 空间转换到 sRGB 空间,是有可能使得中间某个分量小于 0 的。这意味着什么呢?我们把 sRGB 的几个基底画在色品图上,
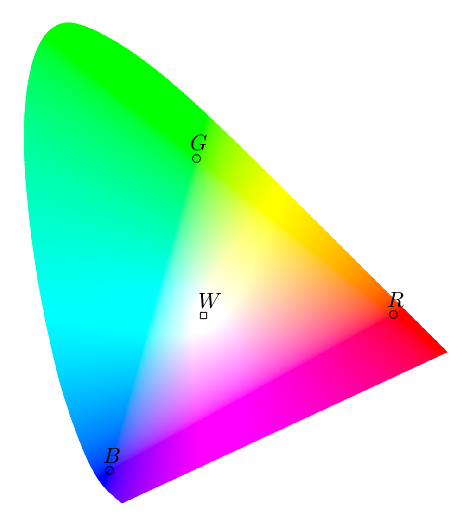
三原色的三个点组成了一个三角形。记得我们反复强调的「锥组合」吗?意味着,sRGB 空间下,所有色彩,都将位于这个三角形内部;转换到三维空间的视角来看,sRGB 空间能表达的色彩,都位于以原点为顶点,连接这个三角形,所有射线围成的锥体内部。如果某个分量小于 0,那么意味着,这个色彩,是落在了这个三角形外部,所以不能被 sRGB 空间所表示出来。一种简单的做法是强制让范围外的值回到范围边界上,让小于 0 的值强制等于 0,让大于 1 的值强制等于 1。这种做法非常简单,计算量也小,但是会损失一些色彩的准确性。在上面的色品图中,可以明显看到有三角形边界的痕迹,三角形之外的色彩,理论上是不能被 sRGB 所表现的,在图中就使用了这种简单的办法处理边界外的情况,相当于用三角形边界上的颜色直接进行了填充。
在前一篇文章中我们看到,在转换完之后,我们只是得到了一个线性的 RGB 值,要被显示器正确显示的话,还需要进行 gamma 校正。每个 RGB 空间对应的 gamma 校正公式不完全一致,大多数情况下都是 C = C_{\text{lin}}^{1/\gamma},其中 γ=2.2,少数情况,比如 Apple RGB 采用的是 γ=1.8 的情况,再比如上面作为举例的 sRGB 空间,采用了一种分段的非线性函数进行校正:
C = \left\{\begin{array}{ll} 12.92C_{\text{lin}} & , \quad C_{\text{lin}} \le 0.0031308 \\[0.6em] 1.055C_{\text{lin}}^{1/2.4} - 0.055 & , \quad C_{\text{lin}} > 0.0031308 \end{array}\right.在粗略的场景下,也可以直接使用 γ=2.2 的公式代替。
到这里,我们已经完全讲明白了从 XYZ 空间到 RGB 空间的转换,不同的 RGB 空间,比如 Adobe RGB 或者 Apple RGB,区别在于三原色与白色点位置不同,一旦这几个基点的位置确定了,那么转换矩阵就完全确定了。中间过程完全是线性变换。
这时候再看上篇文章中的不同色彩空间比较的图,相信就可以读出更多的信息了(下图来自维基百科 RGB Color Space)。

其中 Adobe RGB 与 sRGB 相比较,能表示的颜色要多很多,所以很多摄影师会在相机内设置 Adobe RGB 作为色彩空间。然而现在网络上通用的还是 sRGB,如果不做任何转换,浏览器可能将它视作 sRGB 空间进行渲染,得到的结果就会显得比较灰暗。所以在把图片上传到网络之前,一定要确认色彩空间是否匹配。而在部分专业的色彩输出场合,甚至需要用到 ProPhoto RGB 这种表达能力极强的色彩空间。
4 非线性色彩空间介绍
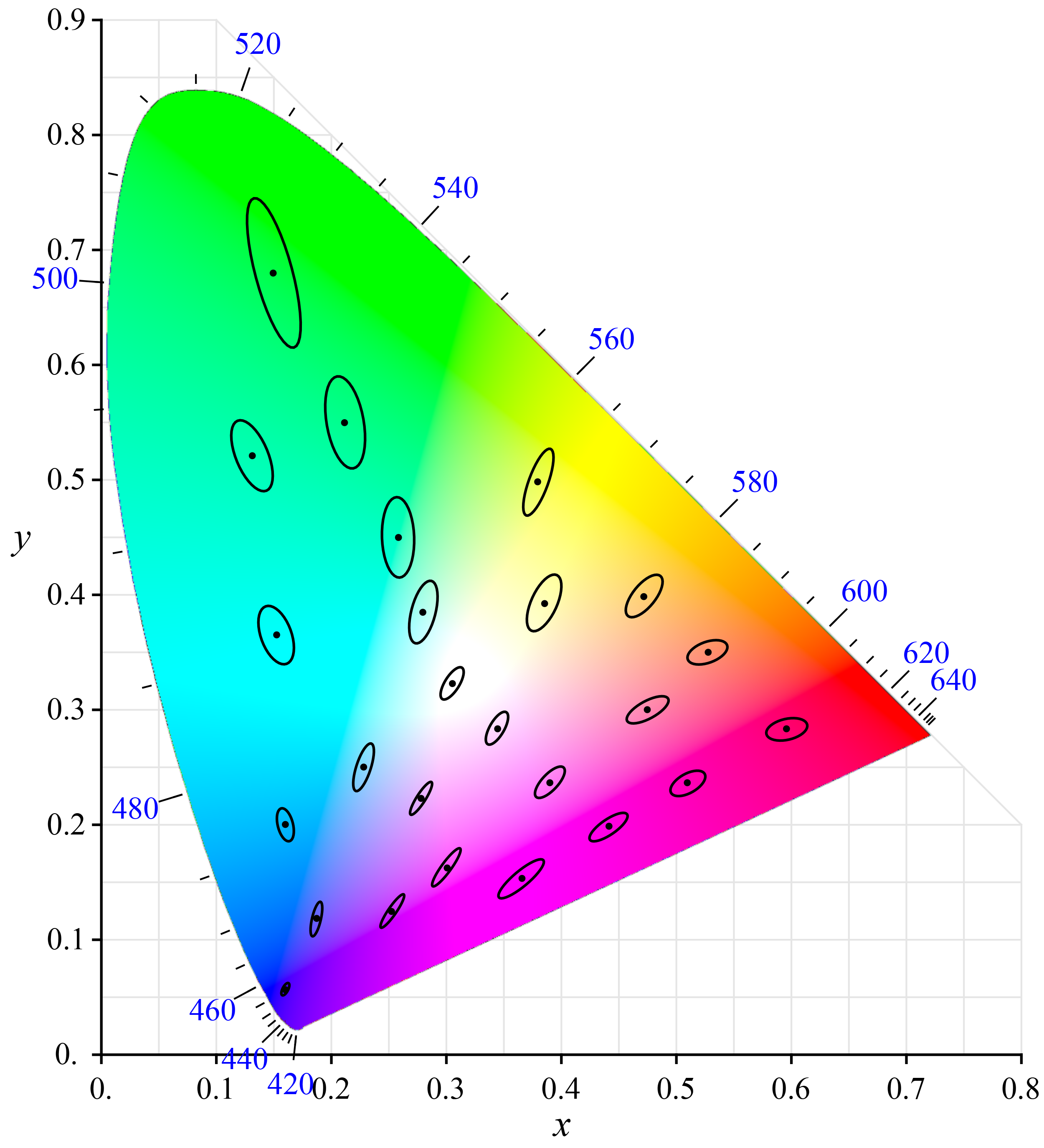
仔细看上面的色品图的边界,可以发现不同波长的光分布的疏密程度是不同的,这意味着在这个空间中,颜色的分布是不均匀的,这种不均匀性是人们不愿意看到的。在 20 世纪 40 年代,麦克亚当(David MacAdam)设计了几个实验,验证了人眼在色彩方面的感知阈值的存在。他的结果被总结为 麦克亚当椭圆(MacAdam ellipse),画在色品图上结果如下 (这里为了展示清楚,图中的椭圆是原始大小的 7 倍,原始数据的结果没有这么夸张。):
这个实验证实了,在一定范围(比如上图中的椭圆)内,人是无法分辨颜色差异的。当然,单纯这样一个结论并不会让人意外,人类对色彩变化的感知总是有限的。这个实验结果重要的意义在于,它直观明了地揭示了 CIE XYZ 这个空间在色彩分布上的不均匀。而麦克亚当椭圆,在这里的意义近似于微分几何中的 度规张量(Metric Tensor),用微分几何的观点来看,从人眼的色彩空间到 CIE XYZ 色彩空间的变换,性质不够好,这将给实际应用带来困难。举个简单的例子,比如由于计算误差或者存储误差,使得颜色分量的值变化了 0.01,如果这个颜色本来是绿色附近的,那变化后的颜色人眼可能根本分辨不出来 (绿色附近的椭圆比较大),如果这个颜色本来是蓝色附近的,那么变化后的颜色人眼就能分辨(蓝色附近的椭圆比较小)。
后来渐渐有更多的科学家研究了人类对色彩的分辨能力,逐渐建立了一些理论基础。人们希望通过一些非线性变换,找到一个「感知均匀性」更好的色彩空间,或者,从微分几何的观点来看,找到一个更为「平坦」的映射关系。比较常用的有 CIE Lab,CIE Luv,等(以下两张图均来自于这两个维基百科页面)。

上图为 CIE Luv 色彩空间的色品图

上图为 CIE Lab 色彩空间三维表示
可以看到,在这两种色彩空间下,色彩的分布更为均匀。
有关这几个空间的性质和计算,就远不是一篇文章可以介绍清楚的了,这里写得太过深入也显得曲高和寡。感兴趣的朋友可以私下交流或者点开链接看看维基百科上的定义。不过这里得提一下,Lab 空间和 Luv 空间在设计的时候就有意让 L 代表明度,也就是把「明度」和「颜色」给分开对待。这就为引入「色相(Hue)」的概念带来了方便,实际上,将这两个空间从直角坐标换成圆柱坐标,马上就可以看到,色相其实就是色彩在圆柱坐标下的角度分量。
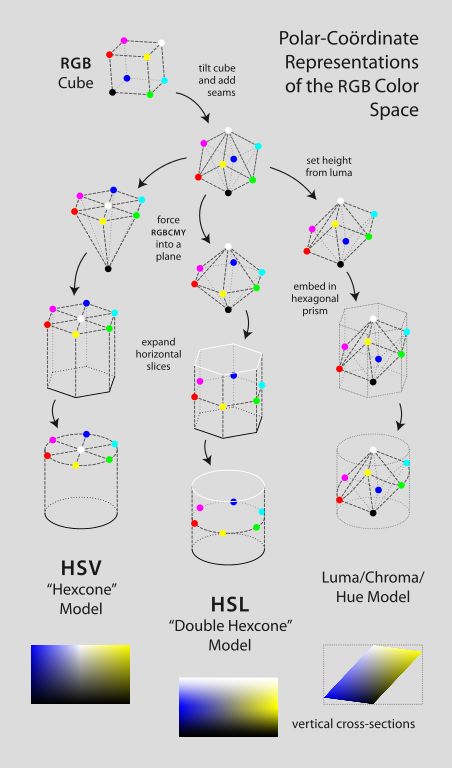
圆柱坐标为人们提供了一个方便的工具,我们学习色彩理论中接触到的「色环」的概念,就来自于此。借助圆柱坐标,人们又从 RGB 空间推导出了 HSV 和 HSL 空间 ,方便不同的用途使用。 (下图来自维基百科 HSV 和 HSL 空间 页面)。
这一些列探索人类色彩感知的实验,直接导致了 颜色差异(Color Difference) 概念的确立,用于表示不同颜色之间的差异性。从微分几何的观点来看,这是在为人类色视觉空间建立一个度规(Metric)。
最后放一个大杀器 CIE 2000 版的颜色差异公式镇场子,这个公式用于衡量两个颜色之间的差异性有多大,
\Delta E^{*} = \sqrt{\left(\frac{\Delta L'}{k_L S_L}\right)^2 + \left(\frac{\Delta C'}{k_C S_C}\right)^2 + \left(\frac{\Delta H'}{k_H S_H}\right)^2 + R_T\frac{\Delta C'}{k_C S_C}\frac{\Delta H'}{k_H S_H}}其中各个符号的定义和计算写下来能写一页纸,这里就不放出来了,感兴趣的朋友可以参照 颜色差异(Color Difference) 的维基页面。
(如无特殊说明,本文所有图片均为我自己绘制或重制)