ECC相关算法解析
前言
近日NSA向微软公布了一个基于ECC加密的漏洞(CVE-2020-0601),该漏洞出现于Windows CryptoAPI(Crypt32.dll)做签名验证的部分,该漏洞可能导致严重的威胁。我对此十分好奇,于是学习了ECC相关的知识,在这里和大家分享一下。
ECC原理介绍
首先我们来学习一下ECC(椭圆曲线加密)的原理。ECC全称为“Ellipse Curve Ctyptography”,是一种基于椭圆曲线数学的公开密钥加密算法。椭圆曲线在密码学中的使用是在1985年由Neal Koblitz和Victor Miller分别独立提出的。与传统的基于大质数分解难题的加密算法不同,该加密方式基于 “离散对数” 这种数学难题。该算法的主要优势是可以使用更小的密钥病提供相当高等级的安全。ECC164位的密钥产生一个安全级,相当于RSA 1024位密钥提供的保密强度,而且计算量较小,处理速度更快,存储空间和传输带宽占用较少。目前我国居民二代身份证正在使用 256 位的椭圆曲线密码,虚拟货币比特币也选择ECC作为加密算法。
一、数学基础
以下内容我们小学二年级就学过,带领大家复习一下

首先我们来介绍一下射影。传统的几何几何系统中,我们可以在《几何原本》中照到如下定理:
- 由任意一点到任意一点可作直线。
- 一条有限线段可以无限延长
- 凡直角皆相等
- 三角形内角和为180度
- 同一平面内一条直线a和另外两条直线b.c相交,若在a某一侧的两个内角的和小于两直角,则b.c两直线经无限延长后在该侧相交

以上内容属于欧式几何,然后又一些大佬觉得欧几里得说的不对,他们觉得第五条定理不能作为公理,而且三角形的内角和也不是180度。所以,有些强者就建立了新的几何体系,比如,俄国的罗巴切夫斯基提出“至少可以找到两条相异的直线,且都通过P点,并不与直线R相交”代替第五公设,然后与欧氏几何的四个公设结合成一个公理系统,简称“罗氏几何(双曲几何)”。黎曼大佬也插了一脚,他觉得“找不到一条直线可以通过P点,并且不与直线R相交”,于是建立了黎曼几何(椭圆几何).数学就是这样神奇,只要你能自圆其说,满足自洽性,你也能建立自己的体系。

我们把上面的两种几何体系称之为非欧几何。定义平行线相交于无穷远点P∞,使平面上所有直线都统一为有唯一的交点,那么:
- 一条直线只有一个无穷远点;一对平行线有公共的无穷远点
- 任何两条直线有不同的无穷远点
- 平面上的无穷远点构成的集合组成一条无穷远直线
射影平面可被认为是个具有额外的“无穷远点”之一般平面,平行线会于该点相交。因此,在射影平面上的两条线会相交于一个且仅一个点。
(一)椭圆曲线
椭圆曲线就是在射影平面上满足魏尔斯特拉斯方程(Weierstrass)的点构成曲线。对于有限域上的椭圆曲线,一般我们用如下方程定义:
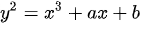
其图像一般如下:
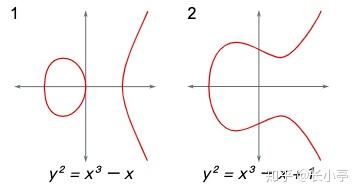
椭圆曲线的定义也要求曲线是非奇异的(即处处可导的)。几何上来说,这意味着图像里面没有尖 点、自相交或孤立点。代数上来说,这成立当且仅当判别式:
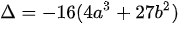
不为0.这里主要是满足其可导性。
(二)近世代数
群
群(group)是由一种集合以及一个二元运算所组成的,并且符合“群公理”。群公理包含下述四个性质的代数结构。这四个性质是:
- 封闭性:对于所有G中a, b,运算a·b的结果也在G中。
- 结合律:对于所有G中的a, b和c,等式 `(a·b)·c = a·(b·c)`成立。
- 单位元:存在G中的一个元素e,使得对于所有G中的元素a,总有等式`e·a = a·e = a`成立。
- 对于集合中所有元素存在逆元素
特殊的群:
满足交换律的群称为交换群(阿贝尔群),不满足交换律的群称为非交换群(非阿贝尔群)。
设 (G, · )为一个群,若存在一G内的元素g,使得
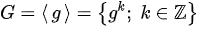
则称G关于运算“ · ”形成一个循环群。
元素的阶(order):
一个群内的一个元素a之阶(有时称为周期)是指会使得am = e的最小正整数m(其中的e为这个群的单位元素,且am为a的m次幂)。若没有此数存在,则称a有无限阶。有限群的所有元素有有限阶。
一个群G的阶被标记为ord(G)或|G|,他表示群内元素的个数,而一个元素的阶则标记为ord(a)或|a|。
有限域
  在数学中,有限域(finite field)或伽罗瓦域(Galois field,为纪念埃瓦里斯特·伽罗瓦命名)是包含有限个元素的域。与其他域一样,有限域是进行加减乘除运算都有定义并且满足特定规则的集合。有限域最常见的例子是当 p 为素数时,整数对 p 取模。有限域的元素个数称为它的阶(order)。可以看出域是满足更多运算的群。
这里我们规定一个有限域Fp
- 取大质数p,则有限域中有p-1个有限元:0,1,2...p-1
- Fp上的加法为模p加法`a+b≡c(mod p)`
- Fp上的乘法为模p乘法`a×b≡c(mod p)`
- Fp上的除法就是乘除数的乘法逆元`a÷b≡c(mod p)`,即 `a×b^(-1)≡c (mod p)`
- Fp的乘法单位元为1,零元为0
- Fp域上满足交换律,结合律,分配律
在这个域上我们希望使用椭圆曲线构造加密函数,但是考虑到曲线本身是连续的,不适合做加密,因此我们得想办法在椭圆曲线上构造一种离散的运算。这是我们可以构造一个阿贝尔群:
给定曲线
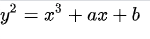
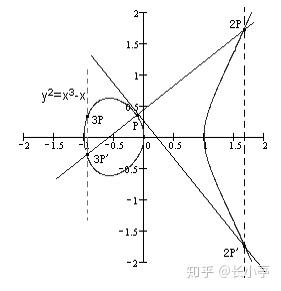
P,Q为曲线上的点,我们规定加法:
实P + Q = R是曲线上点的加法运算,任意取椭圆曲线上两点P、Q(若P、Q两点重合,则作P点的切线),作直线交于椭圆曲线的另一点R',过R'做y轴的平行线交于R,定义P+Q=R。这样,加法的和也在椭圆曲线上,并同样具备加法的交换律、结合律:

若P与Q点重合,则求P的切线交曲线的另一点为R‘。若有k个相同的点P相加,如3P = P + P + P
下面我们利用小学二年级就学过的微积分的知识求一下相关方程:
- 无穷远点 O∞是零元,有O∞+ O∞= O∞,O∞+P=P
- P(x,y)的负元是 (x,-y mod p)= (x,p-y) ,有P+(-P)= O∞
- P(x1,y1),Q(x2,y2)的和R(x3,y3) 有如下关系:
x3≡(k**2-x1-x2)(mod p)
y3≡(k(x1-x3)-y1)(mod p)
这里对等式两边求全微分,即可求出k = dy/dx
若P=Q 则 k=((3x^2+a)/2y1)mod p
这里PQ为不同的点,直接计算斜率
若P≠Q,则k=(y2-y1)/(x2-x1) mod p若kP = O ∞ ,那么k就是点P的阶(order)
这个就是上面群里元素的阶的定义
上面这个椭圆曲线上点的加法运算,就构成了一个阿贝尔群,数学基础到此结束。
二、ElGamal离散对数密码体制
我们来介绍一下基于离散对数的加密算法,首先密钥与公钥的生成步骤如下:
(一)公钥密钥生成:
1. Alice首先构造一条椭圆曲线E,在曲线上选择一点G作为生成元,并求G的阶为n,要求n必须为质数。此时构成了一个循环群\<G>。
2. Alice选择一个私钥k (k < n),生成公钥 Q = kG
3. Alice将公钥组E、Q、G发送给Bob
(二)加密过程
1、Bob收到信息后,将明纹编码为M,M为曲线上一点,并选择一个随机数r(r < n, n为G的阶)
2、Bob计算点Cipher1与Cipher2即两段密文,计算方法如下
- Cipher1 = M + rQ
- Cipher2 = rG
3、Bob把Cipher1和Cipher2发给Alice
(三) 解密过程
1、Alice收到密文后,为了获得M,只需要Cipher1 - k · Cipher2,因为
Cipher1 - k*Cipher2 = M + rQ - krG = M + rkG - krG = M2、将M解码即可
(四)技术要求
在选择参数时有一下要求:
- 大质数p越大安全性越好,但是速度会降低,200位左右可以满足一般安全要求
- n应为质数
- 椭圆曲线上所有点的个数m与n相除的商的整数部分为h,h≤4;p≠n×h ;pt≠1(mod n) (1≤t<20)
- 满足椭圆曲线的判别式
(五)代码实现
接下来我们用python写个简单的demo加深一下理解。
解释一下几个基本函数:
这个函数是扩展欧几里得算法,就是我们常说的辗转相除法求出最大公因数后反向带入的过程,返回最大公因数a和满足
sa + tb = gcd(a,b)(这是贝祖等式)的s0和t0。gcd(a, b)函数的功能是求a,b的最大公因数。
# Extended GCD
def egcd(a, b):
s0, s1, t0, t1 = 1, 0, 0, 1
while b > 0:
q, r = divmod(a, b)
a, b = b, r
s0, s1, t0, t1 = s1, s0 - q * s1, t1, t0 - q * t1
pass
return s0, t0, ainv()这个函数实现了求乘法逆元的功能,使用扩展欧几里得算法。
# Get invert element
def inv(n, q):
# div on ç a/b mod q as a * inv(b, q) mod q
# n*inv % q = 1 => n*inv = q*m + 1 => n*inv + q*-m = 1
# => egcd(n, q) = (inv, -m, 1) => inv = egcd(n, q)[0] (mod q)
return egcd(n, q)[0] % qsqrt()这个函数实现了开平方的算法,需要注意的是这里的乘法运算是有限域上的模乘,因此采用试根的方式。q - i 与 i 构成一对相反数。
def sqrt(n, q):
# sqrt on PN module: returns two numbers or exception if not exist
assert n < q
for i in range(1, q):
if i * i % q == n:
return (i, q - i)
pass
raise Exception("not found")下面我们构造椭圆曲线类EC:
- 构造函数中a,b为EC的参数,p为模p有限域的大质数
- `is_valid(self, p)`判断点p是否在曲线上
- `at(self, x)`,求出党x为横坐标是对应的y值
- `neg(self, p)`,求关于x轴对称的点
- `add(self, p1, p2)`,求点p1,p2在椭圆曲线上的加法
- `mul(self, p, n)`,把p点累加n次
- `order(self, g)`,求g点的阶
# System of Elliptic Curve
class EC(object):
# elliptic curve as: (y**2 = x**3 + a * x + b) mod q
# - a, b: params of curve formula
# - p: prime number
def __init__(self, a, b, p):
assert 0 < a and a < p and 0 < b and b < p and p > 2
assert (4 * (a ** 3) + 27 * (b ** 2)) % p != 0
self.a = a
self.b = b
self.p = p
# just as unique ZERO value representation for "add": (not on curve)
self.zero = Coord(0, 0)
pass
# Judge if the coordinate in the curve
def is_valid(self, p):
if p == self.zero:
return True
l = (p.y ** 2) % self.p
r = ((p.x ** 3) + self.a * p.x + self.b) % self.p
return l == r
def at(self, x):
# find points on curve at x
# - x: int < p
# - returns: ((x, y), (x,-y)) or not found exception
assert x < self.p
ysq = (x ** 3 + self.a * x + self.b) % self.p
y, my = sqrt(ysq, self.p)
return Coord(x, y), Coord(x, my)
def neg(self, p):
# negate p
return Coord(p.x, -p.y % self.p)
# 1.无穷远点 O∞是零元,有O∞+ O∞= O∞,O∞+P=P
# 2.P(x,y)的负元是 (x,-y mod p)= (x,p-y) ,有P+(-P)= O∞
# 3.P(x1,y1),Q(x2,y2)的和R(x3,y3) 有如下关系:
# x3≡k**2-x1-x2(mod p)
# y3≡k(x1-x3)-y1(mod p)
# 若P=Q 则 k=(3x2+a)/2y1mod p
# 若P≠Q,则k=(y2-y1)/(x2-x1) mod p
def add(self, p1, p2):
# of elliptic curve: negate of 3rd cross point of (p1,p2) line
if p1 == self.zero:
return p2
if p2 == self.zero:
return p1
if p1.x == p2.x and (p1.y != p2.y or p1.y == 0):
# p1 + -p1 == 0
return self.zero
if p1.x == p2.x:
# p1 + p1: use tangent line of p1 as (p1,p1) line
k = (3 * p1.x * p1.x + self.a) * inv(2 * p1.y, self.p) % self.p
pass
else:
k = (p2.y - p1.y) * inv(p2.x - p1.x, self.p) % self.p
pass
x = (k * k - p1.x - p2.x) % self.p
y = (k * (p1.x - x) - p1.y) % self.p
return Coord(x, y)
def mul(self, p, n):
# n times of elliptic curve
r = self.zero
m2 = p
# O(log2(n)) add
while 0 < n:
if n & 1 == 1:
r = self.add(r, m2)
pass
n, m2 = n >> 1, self.add(m2, m2)
pass
return r
def order(self, g):
# order of point g
assert self.is_valid(g) and g != self.zero
for i in range(1, self.p + 1):
if self.mul(g, i) == self.zero:
return i
pass
raise Exception("Invalid order")
pass然后我们实现ElGmamal算法
构造函数生成曲线ec,生成元g,以及g的阶n
- `gen(self, priv)`,生成公钥pub
- `enc(self, plain, pub, r)`,把明文plain(已编码为曲线上的点)进行加密
- `dec(self, cipher, priv)`,解密的明文
class ElGamal(object):
# ElGamal Encryption
# pub key encryption as replacing (mulmod, powmod) to (ec.add, ec.mul)
# - ec: elliptic curve
# - g: (random) a point on ec
def __init__(self, ec, g):
assert ec.is_valid(g)
self.ec = ec
self.g = g
self.n = ec.order(g)
pass
def gen(self, priv):
# generate pub key
# - priv: priv key as (random) int < ec.q
# - returns: pub key as points on ec
return self.ec.mul(g, priv)
def enc(self, plain, pub, r):
# encrypt
# - plain: data as a point on ec
# - pub: pub key as points on ec
# - r: randam int < ec.q
# - returns: (cipher1, ciper2) as points on ec
assert self.ec.is_valid(plain)
assert self.ec.is_valid(pub)
return (self.ec.mul(self.g, r), self.ec.add(plain, self.ec.mul(pub, r)))
def dec(self, cipher, priv, public, recv_public):
# decrypt
# - chiper: (chiper1, chiper2) as points on ec
# - priv: private key as int < ec.q
# - returns: plain as a point on ec
self.check(public, recv_public)
c1, c2 = cipher
assert self.ec.is_valid(c1) and ec.is_valid(c2)
return self.ec最后写个main函数验证一下:
if __name__ == "__main__":
# shared elliptic curve system of examples
ec = EC(1, 18, 19)
g, _ = ec.at(7)
assert ec.order(g) <= ec.p
# ElGamal enc/dec usage
eg = ElGamal(ec, g)
# mapping value to ec point
# "masking": value k to point ec.mul(g, k)
# ("imbedding" on proper n:use a point of x as 0 <= n*v <= x < n*(v+1) < q)
mapping = [ec.mul(g, i) for i in range(eg.n)]
plain = mapping[7]
priv = 5
pub = eg.gen(priv)
cipher = eg.enc(plain, pub, 15)
decoded = eg.dec(cipher, priv)
assert decoded == plain
assert cipher != pub
print("Success!")运行结果如下:

三、基于椭圆曲线的数字签名算法ECDSA
签名算法与上面的加密算法类似,下面我们来看一下过程:
- 选择一条椭圆曲线Ep(a,b),和基点G;
- 选择私有密钥k(k<n,n为G的阶),利用基点G计算公开密钥`Q=kG`;
- 产生一个随机整数r(r<n),计算点`R=rG`;
- 密文为message,计算SHA1(message)做为hash;
- 计算`S≡r^-1 *( Hash + k * R.x)(mod n)`; 这里的R.x为R的横坐标
- (R.x, S)做为签名值,如果R和S其中一个为0,重新从第3步开始执行
注:这里的`r^-1`指的是r的乘法逆元
验证签名:
- 接收方在收到消息m和签名值(R.x, S)后,进行以下运算
- 计算明文hash:`hash = SHA1(m)`
- 计算P点:`P = S^-1 *(hash*G + R.x*Q)`
- 若P点的横坐标P.x == R.x,则说明校验成功。
为什么会这样?
下面我们来推导一下:
P = S^{-1} * (hash*G + R.x*Q) ·····1
Q = k*G ·····2
S = r^-1 *(hash + k*R.x) ·····3
R = r*G ·····4
联立1,2,得:
P = S^-1 * (hash + k*R.x)*G ·····5
这时候将3式带入5,即可得:
P = r*G ·····6
这个时候我们对比4,6式,发现了这个神奇的结论:
P = R因此,在校验的时候比较P.x与R.x即可验证签名
我们已经完成数学上的推导,下面我们写个demo实现一下:
- 构造函数初始化椭圆曲线EC,生成元g,生成元的阶n
- `gen(self, priv)`生成公钥Q
- `sign(self, hashval, priv, r)`对hashval进行签名,返回签名(R.x, S)
- `validate(self, hashval, sig, pub)`对签名进行验证,检验hashval是否被篡改
class DSA(object):
# ECDSA
# - ec: elliptic curve
# - g: a point on ec
def __init__(self, ec, g):
self.ec = ec
self.g = g
self.n = ec.order(g)
pass
def gen(self, priv):
# generate pub key
assert 0 < priv and priv < self.n
return self.ec.mul(self.g, priv)
def sign(self, hashval, priv, r):
# generate signature
# - hashval: hash value of message as int
# - priv: priv key as int
# - r: random int
# - returns: signature as (int, int)
assert 0 < r and r < self.n
R = self.ec.mul(self.g, r)
# (R.x, S) S = r^-1 * (hashval + R.x * k)
return (R.x, inv(r, self.n) * (hashval + R.x * priv) % self.n)
def validate(self, hashval, sig, pub):
# validate signature
# - hashval: hash value of message as int
# - sig: signature as (int, int)
# - pub: pub key as a point on ec
assert self.ec.is_valid(pub)
assert self.ec.mul(pub, self.n) == self.ec.zero
# w = S^-1
w = inv(sig[1], self.n)
u1, u2 = hashval * w % self.n, sig[0] * w % self.n
p = self.ec.add(self.ec.mul(self.g, u1), self.ec.mul(pub, u2))
return p.x % self.n == sig[0]
pass我们跑一下下面这段代码试试:
if __name__ == "__main__":
# shared elliptic curve system of examples
ec = EC(1, 18, 19)
g, _ = ec.at(7)
assert ec.order(g) <= ec.q
# ECDSA usage
dsa = DSA(ec, g)
priv = 11
pub = eg.gen(priv)
hashval = 128
r = 7
sig = dsa.sign(hashval, priv, r)
log("sig", sig)
assert dsa.validate(hashval, sig, pub)
print('Success!')
pass
我们可以看到已经验证成功了。
CVE-2020-0601分析
终于到了分析漏洞的时候了,这个漏洞导致的原因其实很简单,我们注意到在生成公钥的一部分`Q = k*G`的时候k我们是不知到的,而且求解难度很大。但是我们在签名的时候需要用私钥签名,怎么伪造签名呢?假如在对公钥做校验的时候我们没有检测G的值,只检查了Q那么我么就可以假装我们知道私钥。此时:
这里的e是乘法单位元,相当于整数乘法里的1
- Q = k*G
- Q' = e*Q = Q
也就是说,我可以直接把“**1**”作为私钥,然后再去签名:
- 公钥:(Q, G)
- 原签名:(R.x,S)
Q = k*G
R = r*Q
S = r^{-1} *(hash + R.x*k)- 伪造公钥:(Q',G')
- 伪造签名:(R'.x, S')
Q' = 1*Q = Q
R' = r*Q' = r*Q
S' = r^{-1} *(hash + R'.x*1)那么我们来分析验证过程:
P = S^{-1} *hash*G + S^{-1} *R.x*Q假如我们把S‘和R‘.x以及公钥(G', Q)代入后可以得到
S’^{-1} = r*(hash + Q.x)^{-1}
P = S'^{-1}*(hash*Q + Q.x*Q)
进一步代入S^-1得:
P = r*(hash + Q.x)^{-1} * (hash + Q.x)*Q = r*Q = R我们看到验证通过。系统在验证公钥得生成元Q == Q‘之后,并没有进一步验证生成元G。这就是**CVE-2020-0601**漏洞利用的原理,crypt32.dll在做校验时,只检查了Q,因此我们用单位元伪造私钥后进行的签名会被验证通过。
下面我们写个脚本验证一下:
if __name__ == "__main__":
# shared elliptic curve system of examples
ec = EC(1, 18, 19)
g, _ = ec.at(7)
assert ec.order(g) <= ec.p
# ECDSA usage
dsa = DSA(ec, g)
# G' = Q = k*G
fake = DSA(ec, ec.mul(g, 11))
# print(g, ec.mul(g, 1))
priv = 11
pub = eg.gen(priv)
# R‘ = r*Q’ = 1 * Q = Q
# 因此fake_pub = pub
fake_pub = pub
log("fake_pub",fake_pub )
log("pub", pub)
hashval = 128
r = 7
# 随机数r设置为不同的值
sig = dsa.sign(hashval, priv, 2)
fsig = fake.sign(hashval, 1, 7)
log("sig", sig)
log("fsig", fsig)
assert sig != fsig
# 分别进行签名校验
assert dsa.validate(hashval, sig, pub)
assert fake.validate(hashval, fsig, fake_pub)
print('Success!')
pass
运行结果如下,我们可以看到用不同的私钥加密获得的签名是不同的,但是由于公钥的生成元G被我们篡改,所以验证也会通过。
最后我们提供一个能用的[poc](https://github.com/ollypwn/cve-2020-0601),仅供学习交流。
总结
这个漏洞的原理其实十分简单,就是小学二年级学过的代数。我们应该注意密码的完整性的校验,更要好好学数学。
参考:
[维基百科](https://zh.wikipedia.org/wiki/ElGamal%E5%8A%A0%E5%AF%86%E7%AE%97%E6%B3%95)
[安全客](简析ECC攻击方法之Pohlig-Hellman - 安全客,安全资讯平台)
[ECC原理解析](ECC椭圆曲线详解(有具体实例) - Kalafinaian - 博客园)

