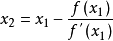如何得到贝塞尔曲线的曲线长度和 t 的近似关系？

这个问题网上 《匀速贝塞尔曲线运动的实现》这篇文章有较完整的解答。不过不够详细，我结合Milo yip大神给出的参考文献详细说明下:

大部分内容都来自这两篇文章，我只添加了自己的理解

二次贝塞尔公式：

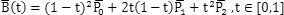
x坐标 X(t) = (1 - t)^2 * p0.x + 2t(1-t) * P1.x + t^2 * p2.x ---------------- (1)

y坐标 Y(t) = (1 - t)^2 * p0.y + 2t(1-t) * P1.y + t^2 * p2.y ---------------- (2)

化简(1) 得： X(t) = (p2.x - 2p1.x + p0.x) * t^2 + (2p1.x - p0.x) * t + p0.x ---- (3)

同理，对y有（4）

为了方便计算, 令 (p2.x - 2p1.x + p0.x) = a.x ; (2p1.x - p0.x) = b.x

即，定义如下变量:

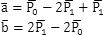
这步是为了(3), (4)表达式不要那么啰嗦.

至此，我们得到(x,y)坐标关于t 和给定点 p0, p1, p2的表达式

我们下一步希望得到移动距离相对于t的表达式

首先对 (3) , (4) 求导，得出在某个点处的瞬时速度:

B'x(t) = 2a.x*t + b.x

B'y(t) = 2a.y*t + b.y

根据平面距离公式，此时速度的大小 s(t) 为：

s(t) = sqrt( (B'x(t))^2 + (B'y(t) ^2) )

s(t) = sqrt( 4a.x^2 * t^2 + 4a.y^2 * t^2 + 4a.x*b.x + 4a.y * b.y + b.x^2 + b.y^2 )

为方便计算，令

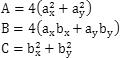
s(t) = sart( At^2 + Bt +C)

至此，我们得到瞬时速度大小关于t 和给定点 p0, p1, p2的表达式

长度就是对于瞬时速度的积分，所以求长度 L(t)即是对 s(t)做积分

感谢伟大的计算机科技，我找到了一个在线计算不定积分的网站:

按照这里的计算:

注意这里算的是不定积分，按定积分算的话还要再减去一个 L(0)

我没有验算这个过程，直接使用的《匀速贝塞尔曲线运动的实现》一文的计算结果:

原文下边这个显然法看不懂，谁看懂了麻烦告诉我...

/*****

设t`就是能够使L实现匀速运动的自变量，那么显然L(t`)=L(1.0)*t，即

*****/

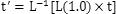
从此处起，我按照Milo yip给出的文献继续进行。

对于游戏应用来说， 问题实际上是： 已知长度， 反求这个长度下的t ， 这样我们可以匀速的滑动长度，求得t，然后再求得坐标

也就是说，已知长度 Distance, 记为D( 由于前边s被当成瞬时速度函数，所以不用这个字母) , 求 L(t) = D 下的 t

即:

已知 L(t) 表达式， L'(t)表达式 （即前文瞬时速度表达式 s(t)）

给定常数D, 令L(t) - D = 0 , 求 t

此问题可以用牛顿切线法近似求解

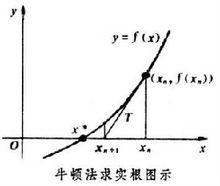
预估一个初始值x0, 对以下表达式迭代即可