矩阵乘法的本质是什么？

评论中 @长江三号 说在b站看到了有关内容,去查了下,确实有一个,而且讲得不错.

贴个链接,感兴趣可以看一看.

线性代数的本质-系列合集
p1 序言
p2 向量究竟是什么
p3 线性组合,张成的空间与基
p4 矩阵与线性变换
p5 矩阵乘法与线性变换复合
p6 三维空间中的线性变换
p7 行列式
p8 逆矩阵,列向量与零空间
p9 非方阵
p10 点积与对偶型
p11 叉积的标准介绍
p12 以线性变换的眼光看叉积
p13 基变换
p14 特征值与特征向量
p15 抽象向量空间
p16 克莱姆法则的几何解释

b站上的学习资源挺多的,有不少深度学习,强化学习等资料,有什么问题去那里查查,说不定有你想要的答案.

第n次提交 2019/9/20　

...

第1次提交 2019/6/25

以下为原回答.

五个角度理解矩阵乘法的本质

• 1.方程组的几何解释
• 2.投影角度的几何解释
• 3.坐标映射的几何解释
• 4.坐标变换的几何解释
• 4.1 缩放
• 4.2 旋转
• 4.3 平移
• 4.4 一般矩阵的缩放与旋转分解
• 4.4.1 对称矩阵
• 4.4.2 一般矩阵
• 5.行列式变换的代数解释

写在前面

在机器学习算法中，矩阵相乘非常常见。对矩阵乘法这种底层操作进行分析，有时候可以帮助我们更好地理解算法。那矩阵乘法的本质到底该怎样理解呢？

针对这个问题，我查阅了很多资料，写了一篇总结的博客，思考了很久，也整理了很久．大体上可以分为5个角度来解读，现整理如下，分享给大家。

需要说明的是，1,2,3,4对矩阵乘法的分析都是向量左乘矩阵，当然这很容易扩展到矩阵相乘，但是不免有一些局限性，只能说提供一些思考的思路。

声明：编辑的时候没有太好的引用格式，我就采用了加斜体和给原文链接的方式。本文第3部分除最后一张，其他图片均来自[2]．第４部分除了我的手推公式，其他图片均来自[4]．

1. 方程组的几何解释

“矩阵最初的目的，只是为线性方程组提供一个简写形式”[1]． 一个矩阵可以看成方程组的系数。我们来看这样一个方程组：

在x,y坐标轴中，画出这两个方程对应的图像，如下图：

很容易发现，两条直线的交点就是方程组的解，也就是矩阵乘法的解。

从方程组的角度来解释，矩阵A可以看成方程组的系数，一个矩阵对应唯一的一个方程组。向量X左乘矩阵A就是方程组的简化记法。

显然向量X的各属性取不同的值，我们就得到了不同的组合，不同组合的结果会显示在结果矩阵中。如果X看成药材，那么A就可以看成药材的配比组合。不同的药材使用相同的配比阵(映射)A,得到几种不同的配方。

所以这里左乘的矩阵A也可以看成一个线性映射关系，矩阵中的每个值表示线性映射的映射系数(这个词乱扯的，大家明白什么意思就行).从数学意义上说,向量X左乘矩阵A就相当于对X进行线性映射[11].

2. 投影角度的几何解释

如何在空间中确定一个向量呢？在空间中设立一个坐标系（设立一组基），这里的基是一些线性不相关的向量。当然这里我们需要表示一个n维物体的时候我们就需要找到n个n维的向量，这n个线性无关的向量是一个坐标系的确定表示。所以n个线性无关的向量组成的n阶方阵，我们可以认为它是一个坐标系。投影解释就是从这个角度出发的。

考虑AB=C，其中A(R,N), B(N,M), C(R,M)为矩阵。

我们首先看下向量的点乘： a_{i}b_{j}=|a_{i}| * |b_{j}| * |cos(a_{i},b_{j})|。如果令 |a_{i}|=1, a_{i}b_{j} 就是 b_{j} 在 a_{i} 上的投影。其实我们常用的向量的坐标就是向量在各单位基向量上的投影值。

当R=N时且满秩时，A可以看成一个坐标系，A的每一行代表这个坐标系的一个基。A*B可以看成是B的每一个列向量 b_{j}在A的每一个行向量 a_{i}(基向量)上进行投影，当A的每一个基模都为1时，投影的结果恰好就是B在A坐标系中的坐标值。

而对一般情况，A不一定能代表坐标系，我们可以把矩阵相乘看成将右边矩阵的每一列向量投影(映射)到以左边矩阵R个行向量所表示的空间中去。 @deng will 大佬对这一块解释得更好[3]，这里我们直接把原文搬过来。

当然在二维平面我们默认选择(1,0)和(0,1)为单位向量，这样二维平面上坐标和向量就是直接对应，非常方便。实际上任意两个线性无关（二维空间可以看成不在一条直线上）的向量都可以成为一组基，而且除以向量的模都可以使模变为1。
一般的，如果我们有M个N维向量，想将其变换为由R个N维向量表示的新空间中，那么首先将R个基按行组成矩阵A，然后将向量按列组成矩阵B，那么两矩阵的乘积AB就是变换结果，其中AB的第m列为B中第m列变换后的结果。

这种从一个空间到另一个空间的变换关系,从更抽象的角度来说,就是数学意义上的线性映射[10].

3. 坐标映射的几何解释

坐标映射是比较形象的一种角度，我们来看个例子吧．对于下面的矩阵乘法：

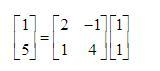
这里由于向量的模全为1，所以直接从图上不容易看出来。首先来看下，横轴和纵轴的单位向量在矩阵乘法之后对应的向量分别是什么？[2]中解释得非常棒，我们搬运原文：

对于横轴单位向量(1,0)，有

对于纵轴单位向量(0,1)，有

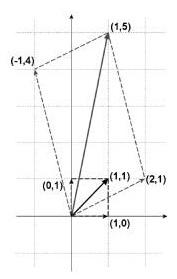
结论一目了然，对于横轴，也就是第一个维度的单位向量，变换后对应的就是变换矩阵的第一列的列向量(2,1)，对于纵轴，也就是第二个维度的单位向量，变换后对应的就是变换矩阵的第二列的列向量(-1,4)。这个结论可以很容易地推广到高维情况，对于第i维度的单位向量，变换后对应的就是变换矩阵中的第i列的列向量。
可以把这种变换形象地理解成一种坐标的映射，具体到本例，就是上图中的情况，经过变换后原来的(1,0)对应的新坐标是(2,1)，(0,1)对应的新坐标是(-1,4)。在这种对应关系下，考虑由(0,0)，(1,0)，(1,1)和(0,1)围起来的单位长度的小方框，经过变换后相当于被“拉伸”成为由(0,0)，(2,1)，(1,5)和(-1,4)围起来的四边形，所以在单位方框中右上角的顶点，在变换后就是被拉伸后四边形的对应顶点(1,5)。

从坐标映射的角度来说，向量左乘矩阵是把向量各分向量变换到新的位置(对每一维的坐标进行映射), 然后通过向量加法(采用代数加法实现)得到结果。

所以对于AX=b，相当于A的各列通过某种线性组合得到b.也就是说，b向量在A矩阵的列空间中。哈哈有意思吧。

4. 坐标变换的几何解释

矩阵可以看作是对运动的描述。矩阵的几何意义，可以拆分为三个特性。

4.1 缩放

我们来看一个矩阵的缩放实例：

一个向量左乘对角阵相当于对向量各维坐标值进行缩放，缩放的比例就是对角阵元素的值。当然了，这里的向量缩放这里也可以看成坐标轴进行缩放，两者是等价的。为什么这么说呢？

如上图所示，可以理解为对基向量进行了缩放，即对坐标轴进行了缩放。对角阵都可以看成是缩放矩阵。

4.2 旋转

首先看一个旋转的实例：

显然左乘这个矩阵相当于把(1,1)向量顺时针旋转45度，相当于把坐标轴逆时针旋转45度。向量旋转和矩阵旋转正好是方向相反的。从这个例子出发，我们可以得出沿坐标轴旋转的一些通用矩阵。下面三个矩阵表示向量绕X,Y和Z轴的顺时针旋转θ度，或者说坐标轴绕X,Y和Z轴逆时针旋转θ度：

看成坐标轴旋转时各向量位置不变；而看成向量旋转时坐标轴是固定的，此时从几何直观上讲，只有坐标轴上的向量还在原来的方向上。

4.3 平移

让我们看一个小例子。如果我们想将点(10,5,0)移动(-8,2,4)。可以这样做：

第4个坐标没有几何意义，它只是让我们可以定义一个平移矩阵。
你会注意到有时这个常量不是1。事实上，通用规则是只需简单地将X,Y和 Z 坐标除以第4个坐标，我们将第4个坐标称之为W坐标。 简单地说：(20,10,0,2) = (10,5,0,1)，这两个坐标表示的是同一个3D点(10,5,0)，所以从4个坐标中获取3D点的简单规则是：

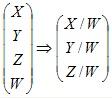
第四维坐标只是帮助我们可以定义一个平移矩阵，类似于平面几何的辅助线的作用。这里其实平移矩阵中增加第四列就已经够了，不需要再增添一行，可以简化成下列形式：

我们作进一步的拆分，如下：

其实，这也可看成回归拟合问题y=AX+b. X左乘矩阵A只能实现伸缩和旋转，而加上位移后，则可以轻松实现拟合。拟合的系数矩阵为A。

这个位移向量偏置在机器学习中是一种常见的参数，通常被称为偏置（bias），而形如y=Ax+b的变换形式也是机器学习中最常见的变换，称做仿射变换。简单来说，仿射变换就是一个线性变换接着一个位移。
从拟合的角度看，偏置对结果的影响主要和样本的分布相关，一般来说当样本方差大、维度高的时候，则偏置的影响就会小一些。偏置的引入让变换的灵活度更大，但却不再是线性变换，并且形式上变得比y=Ax更复杂。

4.4 一般矩阵的缩放与旋转分解

这部分的内容将矩阵乘法延伸到了SVD，查了这么多资料都没有讲这个。我去，想了好久才想明白，发际线又倒退了，我何苦要想这个无聊的问题。

好的，我们已经知道，矩阵可以看作是对运动的描述。矩阵的几何意义，可以拆分为三个特性：伸缩，旋转和平移。其中平移需要扩维暂且不谈。所以矩阵的主要特性就是伸缩和旋转。很多矩阵都可以拆分为这两个特性的组合。

4.4.1 对称矩阵

我们先从特例对称矩阵看起，看个实例吧：

我们可以发现，向量在 x^{'} 方向上进行了3倍的拉伸，在 y^{'} 方向保持不变。我们可以把这个乘法看成将坐标轴逆时针旋转θ=45度，在x轴方向将向量拉伸3倍，然后再把坐标轴转回来。也就是：

从图片中我们得知，可以从坐标轴旋转和投影两个角度进行思考，其实效果都是一样的。我们将系数矩阵A进行分解，得到：

好的，我们总结下A的分解过程： X_{1}=U^{T}X 是将X投影到坐标系U中，由于U是正交矩阵(基的模为1)，所以获得的是X在U中的坐标，也就是将坐标轴旋转后的坐标 X_{1} ；(旋转)

X_{2} = SX_{1} 是将X在新坐标系中，沿着坐标轴方向进行拉伸；(拉伸)

A = UX_{2}是将向量X从新坐标系统映射回原坐标系。因为U为正交矩阵，所以 U^{T} = U^{-1} , UX_{2} = (U^{T})^{T}X_{2} = (U^{-1})^{T}X_{2} ，根据前面投影的分析我们知道， (U^{-1})^{T}X_{2} 是将 X_{2} 映射到 U^{-1} 所表示的坐标轴中，坐标轴U下的 U^{-1} 就是原先的坐标轴。所以这里就是把X从新坐标轴投影回去，或者说将坐标轴旋转回去。得到的是在原坐标系中的坐标。(转回来)

A = USU^{T} 其实就是对A进行特征值分解。我们可以推广到一般形式：若A为n阶实对称矩阵，则存在正交矩阵U和对角阵S使得 A = USU^{-1}，其中S对角线的元素是A的特征值，U的列向量为A的特征向量。（只推广到实对称矩阵，没有推广到可对角化矩阵）

=====================================================

4.4.2 一般矩阵

所有的实矩阵都可以拆分出旋转和缩放的效果。上面讲的是实对称矩阵可以进行特征值分解，得到正交特征向量矩阵，效果是先旋转然后缩放然后转回来，非对称实矩阵能不能也这样拆分呢？ 假设可以，那么对于非对称实矩阵A，一定存在正交矩阵U，使得A=UVUT。

A不是方阵显然已经不行。A是方阵时我们随便看个特例。实际上对于二维矩阵A，我们这样分解的时候，只有a,b,θ三个变量，而A有四个元素，可以构建四个方程直接求解。随便找一个自己试试就知道是无解的。那该如何拆分呢？非要拆分为旋转和缩放的话就需要SVD拆分。

这里需要声明一下，并不是非对称实矩阵A就不能进行特征值分解，只要实矩阵A是可对角化矩阵都可以进行特征值分解。这里讲的是拆分为旋转和缩放，对于非对称实矩阵A，得到的U不是正交矩阵，而原先默认的坐标系x,y,z..是正交坐标系，这种情况不能像对称矩阵那样，得到旋转和缩放的效果。

为什么非对称实矩阵不能像实对称矩阵一样分解呢？因为非对称实矩阵不能找到一组正交基(无解)，使得矩阵相乘达到只在这组正交基的基向量上进行缩放。所以先找到一个可以在基向量方向直接缩放的坐标系，缩放完成然后转回来这种方案不可行，因为它转不回来了。

用A代表这个矩阵，它可以用SVD分解为 A=USV^{T} ，在matlab中的分解结果为：

这相当于先将向量顺时针旋转58.3°，然后在x和y方向缩放1.618和0.618倍，再逆时针旋转31.7°，从这里我们发现，非对称实矩阵A并没有将向量转回去。

上述实例A是非对称实矩阵,但是个方阵,还不能代表一般情况.当A不是方阵呢?

A不是方阵,使用SVD拆分为旋转和缩放的同时,也会有一个维度(空间)的变换.这里简单提下,感兴趣的可以继续阅读6个层面透彻理解奇异值分解的第三章.

对于4.4节的内容，说实话有点难懂，我想了好久才想出来。然后就在网上找到了马同学的分析，尼玛真是相见恨晚！马同学我要是早看到你的分析就不用自己想这么久了。。。推荐[8][9]。

5. 行列式变换的代数解释

之前的四部分都是把矩阵相乘简化为向量左乘矩阵进行分析。如果从整体看的话，初等矩阵左乘，相当于行变换，初等矩阵右乘，相当于列变换。这个大家在学习线性代数的时候应该都了解过，就不多说了。

参考

[1] https://www.cnblogs.com/hejunlin1992/p/7702858.html

[2] http://book.51cto.com/art/201711/558142.htm?from=singlemessage

[3] https://www.zhihu.com/question/28623194?sort=created

[4] https://www.cnblogs.com/luxishi/p/6668838.html

[5] https://www.cnblogs.com/lzllovesyl/p/5243370.html

[6] https://blog.csdn.net/u010916338/article/details/85112084

[7] 任广千谢聪胡翠芳. 线性代数的几何意义[M].

[8] https://www.matongxue.com/madocs/228/

[9] https://www.matongxue.com/madocs/555/

[10] https://zh.wikipedia.org/wiki/%E7%BA%BF%E6%80%A7%E6%98%A0%E5%B0%84

[11] https://baike.baidu.com/item/%E7%BA%BF%E6%80%A7%E5%8F%98%E6%8D%A2

公众号

更多精彩内容:推荐算法工程师

7分钟入门线性代数+微积分https://www.zhihu.com/video/1045055752112746496

这是一个系列短片，若感兴趣，观看顺序是：

• 学习观01：好多人一辈子都没搞清什么是学习
• 学习观02：什么叫“先把书读厚，再把书读薄”
• 学习观03：其实你早就学会了“英语”
• 学习观04：为什么会觉得编程、解题毫无头绪
• 学习观4.5：这些学习方法从何而来？
• 学习观05：思维导图原理：人生与高手之差
• 学习观5.5：怎么设计你自己的思维导图画法
• 学习观06：为什么费曼技巧被称为终极学习法
• 学习观07：如何正确使用人脑来在几个月内学会英语
• 超智能体01：高考与机器学习
• 超智能体02：线性代数与微积分
• 超智能体03：9分钟入门深度学习

若没跟上，可看如何生动有趣的入门线性代数