hash算法的数学原理是什么，如何保证尽可能少的碰撞？

原表达式实际上是

hash = (\sum_n a[n] s^n) \mod 2^{31}

a是str，s是seed。

这个哈希函数的好坏首先取决于s^n \mod 2^{31}这个序列的循环周期，如果周期很短的话，周期之后的字符就会乘以和前面的某个对应字符相同的系数，这样很容易产生碰撞。当s是奇数的时候，s与2^{31}互质，考虑序列s, 3s, 5s, 7s, ..., (2^{31} - 1)s，这其中任意两个数的差都至多是2^{31} - 2倍的s，而s与2^{31}互质，因此序列中任意两个数对2^{31}取模后不相等。一共有2^{30}个不同的结果，而这些结果都是奇数，因此必然与1,3,5,...,2^{31} - 1一一对应。我们把所有的数相乘，由于系数都是奇数，因此系数的乘积与2^{31}互质，消去系数就得到：

s^{2^{30}} \equiv 1 \pmod {2^{31}}

说明周期至多是2^{30}然而还没有这么简单，考虑s^{2k}形式的数，它是s^k的平方。由于

(2^{30} + m)^2 = 2^{60} + 2^{31}m + m^2 \equiv m^2 \pmod {2^{31}}

(2^{30} - m)^2 = 2^{60} - 2^{31}m + m^2 \equiv m^2 \pmod {2^{31}}

因此

s^2, s^4 , s^6, ..., s^{2^{30}}

最多只有2^{28}个不同的可能结果，因此其中至少有两个数是同余的，说明周期小于2^{30}，而且是它的因子，所以周期最多是2^{29}

s^{2^{29}} \equiv 1 \pmod {2^{31}}

所以我们可以认为这个hash函数足够好的条件是：

1. s是奇数
2. s^{2^{28}} \ne 1 \pmod {2^{31}}

不是所有的奇数都满足第二条，但是131是满足的。至于后面备选的那些，我也不明白为什么跟1和3过不去，实际上1313并不满足第二条，而满足的也不一定跟13有多大关系，比如说267也是满足的。其中是不是有什么深刻的道理在我就不是很清楚了。

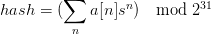
我来解释一下为什么s一般取值为131，使用为前面的字符串数组a[n]中，取得的字符的为ascii码，数值<=127，为了尽可能保证获取的hash值的唯一性，因此需要让s为一个大于127的质数，而为了提高散列密度，又要使s尽可能小，因此，大于127的最小质数，就是131。这个值具有最佳的散列质量和散列密度。

知乎首次认真回答，望多多给赞