Description
乱序
乱序的意思就是将数组打乱。
嗯,没有了,直接看代码吧。
Math.random
一个经常会遇见的写法是使用 Math.random():
var values = [1, 2, 3, 4, 5];
values.sort(function(){
return Math.random() - 0.5;
});
console.log(values)Math.random() - 0.5 随机得到一个正数、负数或是 0,如果是正数则降序排列,如果是负数则升序排列,如果是 0 就不变,然后不断的升序或者降序,最终得到一个乱序的数组。
看似很美好的一个方案,实际上,效果却不尽如人意。不信我们写个 demo 测试一下:
var times = [0, 0, 0, 0, 0];
for (var i = 0; i < 100000; i++) {
let arr = [1, 2, 3, 4, 5];
arr.sort(() => Math.random() - 0.5);
times[arr[4]-1]++;
}
console.log(times)测试原理是:将 [1, 2, 3, 4, 5] 乱序 10 万次,计算乱序后的数组的最后一个元素是 1、2、3、4、5 的次数分别是多少。
一次随机的结果为:
[30636, 30906, 20456, 11743, 6259]该结果表示 10 万次中,数组乱序后的最后一个元素是 1 的情况共有 30636 次,是 2 的情况共有 30906 次,其他依此类推。
我们会发现,最后一个元素为 5 的次数远远低于为 1 的次数,所以这个方案是有问题的。
可是我明明感觉这个方法还不错呐?初见时还有点惊艳的感觉,为什么会有问题呢?
是的!我很好奇!
插入排序
如果要追究这个问题所在,就必须了解 sort 函数的原理,然而 ECMAScript 只规定了效果,没有规定实现的方式,所以不同浏览器实现的方式还不一样。
为了解决这个问题,我们以 v8 为例,v8 在处理 sort 方法时,当目标数组长度小于 10 时,使用插入排序;反之,使用快速排序和插入排序的混合排序。
所以我们来看看 v8 的源码,因为是用 JavaScript 写的,大家也是可以看懂的。
源码地址:https://github.com/v8/v8/blob/master/src/js/array.js
为了简化篇幅,我们对 [1, 2, 3] 这个数组进行分析,数组长度为 3,此时采用的是插入排序。
插入排序的源码是:
function InsertionSort(a, from, to) {
for (var i = from + 1; i < to; i++) {
var element = a[i];
for (var j = i - 1; j >= from; j--) {
var tmp = a[j];
var order = comparefn(tmp, element);
if (order > 0) {
a[j + 1] = tmp;
} else {
break;
}
}
a[j + 1] = element;
}
};其原理在于将第一个元素视为有序序列,遍历数组,将之后的元素依次插入这个构建的有序序列中。
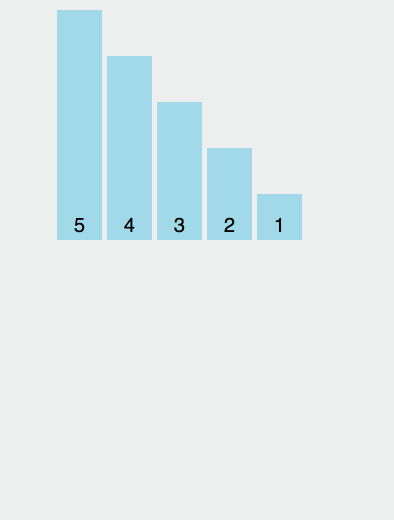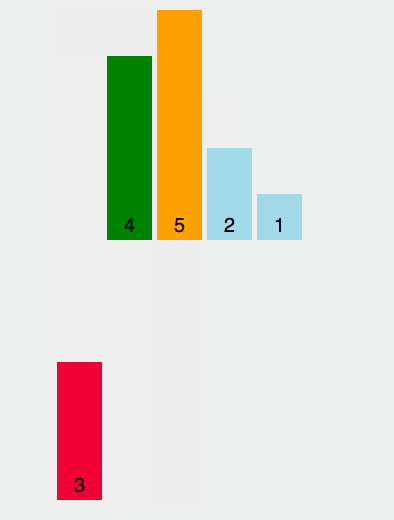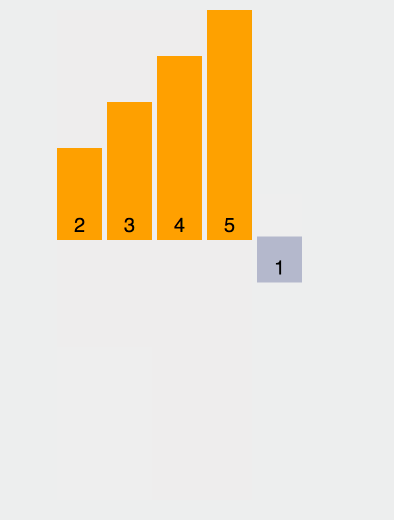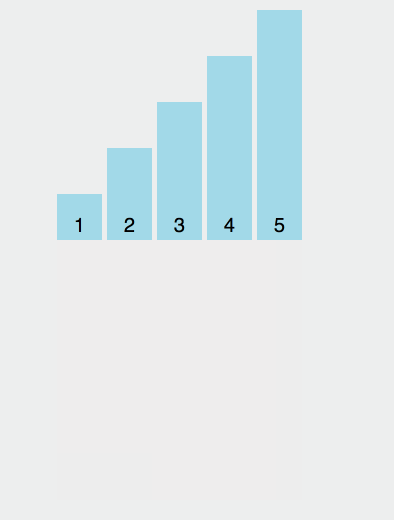
我们来个简单的示意图:
具体分析
明白了插入排序的原理,我们来具体分析下 [1, 2, 3] 这个数组乱序的结果。
演示代码为:
var values = [1, 2, 3];
values.sort(function(){
return Math.random() - 0.5;
});注意此时 sort 函数底层是使用插入排序实现,InsertionSort 函数的 from 的值为 0,to 的值为 3。
我们开始逐步分析乱序的过程:
因为插入排序视第一个元素为有序的,所以数组的外层循环从 i = 1 开始,a[i] 值为 2,此时内层循环遍历,比较 compare(1, 2),因为 Math.random() - 0.5 的结果有 50% 的概率小于 0 ,有 50% 的概率大于 0,所以有 50% 的概率数组变成 [2, 1, 3],50% 的结果不变,数组依然为 [1, 2, 3]。
假设依然是 [1, 2, 3],我们再进行一次分析,接着遍历,i = 2,a[i] 的值为 3,此时内层循环遍历,比较 compare(2, 3):
有 50% 的概率数组不变,依然是 [1, 2, 3],然后遍历结束。
有 50% 的概率变成 [1, 3, 2],因为还没有找到 3 正确的位置,所以还会进行遍历,所以在这 50% 的概率中又会进行一次比较,compare(1, 3),有 50% 的概率不变,数组为 [1, 3, 2],此时遍历结束,有 50% 的概率发生变化,数组变成 [3, 1, 2]。
综上,在 [1, 2, 3] 中,有 50% 的概率会变成 [1, 2, 3],有 25% 的概率会变成 [1, 3, 2],有 25% 的概率会变成 [3, 1, 2]。
另外一种情况 [2, 1, 3] 与之分析类似,我们将最终的结果汇总成一个表格:
| 数组 | i = 1 | i = 2 | 总计 |
|---|---|---|---|
| [1, 2, 3] | 50% [1, 2, 3] | 50% [1, 2, 3] | 25% [1, 2, 3] |
| 25% [1, 3, 2] | 12.5% [1, 3, 2] | ||
| 25% [3, 1, 2] | 12.5% [3, 1, 2] | ||
| 50% [2, 1, 3] | 50% [2, 1, 3] | 25% [2, 1, 3] | |
| 25% [2, 3, 1] | 12.5% [2, 3, 1] | ||
| 25% [3, 2, 1] | 12.5% [3, 2, 1] |
为了验证这个推算是否准确,我们写个 demo 测试一下:
var times = 100000;
var res = {};
for (var i = 0; i < times; i++) {
var arr = [1, 2, 3];
arr.sort(() => Math.random() - 0.5);
var key = JSON.stringify(arr);
res[key] ? res[key]++ : res[key] = 1;
}
// 为了方便展示,转换成百分比
for (var key in res) {
res[key] = res[key] / times * 100 + '%'
}
console.log(res)这是一次随机的结果:
我们会发现,乱序后,3 还在原位置(即 [1, 2, 3] 和 [2, 1, 3]) 的概率有 50% 呢。
所以根本原因在于什么呢?其实就在于在插入排序的算法中,当待排序元素跟有序元素进行比较时,一旦确定了位置,就不会再跟位置前面的有序元素进行比较,所以就乱序的不彻底。
那么如何实现真正的乱序呢?而这就要提到经典的 Fisher–Yates 算法。
Fisher–Yates
为什么叫 Fisher–Yates 呢? 因为这个算法是由 Ronald Fisher 和 Frank Yates 首次提出的。
话不多说,我们直接看 JavaScript 的实现:
function shuffle(a) {
var j, x, i;
for (i = a.length; i; i--) {
j = Math.floor(Math.random() * i);
x = a[i - 1];
a[i - 1] = a[j];
a[j] = x;
}
return a;
}原理很简单,就是遍历数组元素,然后将当前元素与以后随机位置的元素进行交换,从代码中也可以看出,这样乱序的就会更加彻底。
如果利用 ES6,代码还可以简化成:
function shuffle(a) {
for (let i = a.length; i; i--) {
let j = Math.floor(Math.random() * i);
[a[i - 1], a[j]] = [a[j], a[i - 1]];
}
return a;
}还是再写个 demo 测试一下吧:
var times = 100000;
var res = {};
for (var i = 0; i < times; i++) {
var arr = shuffle([1, 2, 3]);
var key = JSON.stringify(arr);
res[key] ? res[key]++ : res[key] = 1;
}
// 为了方便展示,转换成百分比
for (var key in res) {
res[key] = res[key] / times * 100 + '%'
}
console.log(res)这是一次随机的结果:
真正的实现了乱序的效果!
专题系列
JavaScript专题系列目录地址:https://github.com/mqyqingfeng/Blog。
JavaScript专题系列预计写二十篇左右,主要研究日常开发中一些功能点的实现,比如防抖、节流、去重、类型判断、拷贝、最值、扁平、柯里、递归、乱序、排序等,特点是研(chao)究(xi) underscore 和 jQuery 的实现方式。
如果有错误或者不严谨的地方,请务必给予指正,十分感谢。如果喜欢或者有所启发,欢迎 star,对作者也是一种鼓励。


Activity
Izayoih commentedon Oct 18, 2017
学到了.....我是用了好久第一个方法现在才意识到这个问题....
最终方案的话其实理论上会有可能shuffle结果和原数组相同的情况,但是数组长度比较长的话就可以忽略不计。
如果考虑到欧皇的人品,是不是shuffle完判断一下好一点....
mqyqingfeng commentedon Oct 18, 2017
@lzayoih 确实会有可能与原数组相同,如果有这个需求,一定要与原数组不一样,确实需要再判断一次~
zhaowenjie commentedon Oct 25, 2017
深度好文,顶一下,赞一下楼主做的gif图,简单明了,生动形象
mqyqingfeng commentedon Oct 25, 2017
@zhaowenjie 谢谢夸奖,其实这个演示的动画来自于 https://visualgo.net/en/sorting,有各种排序算法的演示动画,我只是录制了一个 gif ~
scutuyu commentedon Oct 26, 2017
not bad
zhangruinian commentedon Nov 20, 2017
my brother niubility
HuangQiii commentedon Nov 20, 2017
这篇文章写的很好,特别喜欢那个图=。=
附上我当时的测试代码,因为楼主的判断是第四位出现每个数字的次数,我觉得可以有个更直观的呈现,附上代码:
对了忘了注释。count[n][i]是数字n在i出现的次数
可以直接到控制台去跑,会花一点点时间
会出现两个图表
可以看到,表一的值很平均(更乱)
表二的对角线的概率大一点
最后,有个网站蛮直观的,这个
点击这个看看分布图,然后看看他给出的代码,聪明的你会理解更深刻
mqyqingfeng commentedon Nov 21, 2017
@HuangQiii 感谢补充,非常的赞~ o( ̄▽ ̄)d
iiicon commentedon Feb 6, 2018
这样我才能懂。我是不适合看源码吗 😢
D-kylin commentedon Mar 23, 2018
其实乱序我还是更倾向于只用Math.random来辅助替换元素达到乱序,其实仔细想想排序的结果,都会出现某些元素已经排序好而固定位置,那么剩余的元素就一定会因为排序操作而有更多的机会参与“乱序”,造成结果的不平均。
mqyqingfeng commentedon Mar 28, 2018
@iiicon 哈哈,本质上都是一样的,知道是用来干什么的以及大致是如何实现的就可以啦~
22 remaining items